Wouldn’t it be nice to be able to predict something that is important to you? Sure—and it would be extra nice if you knew how accurate your predictions will be. Well, you don’t have to be a psychic to have these powers because Minitab Statistical Software gives them to you! You can find these predictive powers in regression, general linear model (ANOVA), and the design of experiments (DOE).
Prediction with Regression Analysis
We’ll explore prediction with regression analysis by using a person’s body mass index (BMI) to predict their percentage of body fat. For extra fun, we’ll compare Minitab’s predictions to those reported by body fat measuring scales that use bioelectrical impedance analysis (BIA).
Prediction in Minitab is different from the psychic ability. For one thing, you are often not predicting the future, which is the case with this blog’s example. Prediction in regression refers to estimating the value of one variable using assumed values of other input variables that are related to it.
Unlike psychic ability, statistical predictions don’t just pop into your head. Instead, you need to collect data and develop a mathematical model that describes the relationship between one or more variables and the variable you want to predict. The accuracy of your predictions depends on how well your model fits the data. In exchange for this work, Minitab not only predicts but also gives you estimates of their accuracy!
The steps for accurate prediction are:
- Do background research so you know what you’re doing!
- Collect the data.
- Fit and evaluate competing regression models.
- Determine the best model.
- Predict!
Scenario
I’ve already collected the data from 92 middle-school-aged girls. The data includes their height, weight, and percentage of body fat as measured by a Hologic DXA whole-body system. DXA measurements are considered one of the best ways to measure the percentage of body fat. You can get the data here.
The idea here is that DXA measurements are more expensive and harder to obtain than your BMI. It would be great if you could use your BMI to predict your percentage of body fat. BMI is a general assessment of whether your weight is in an appropriate range for your height. However, BMI is an imperfect measure because it cannot distinguish between weight from muscle versus weight from fat. Therefore, a goal of this analysis is to see if BMI is good enough.
Regression Model
For this blog, I’ve already reduced the model down to the final form. The process of reducing the model is the subject of another blog, but now I will show you why the final model is a good one. During that process, I specifically compared including height, weight, and their squared terms in the model to including BMI and its squared term in the model. I included the squared terms in order to model the curvature. Both approaches produced nearly identical results. This isn’t surprising because you use height and weight to calculate BMI (weight in kilograms/height in meters squared). I’ve decided to use BMI as the predictor because it’s easier to graph in the results below.
Because we have one predictor (BMI) and one response (Body Fat Percentage), we can use a fitted line plot to display the relationship.
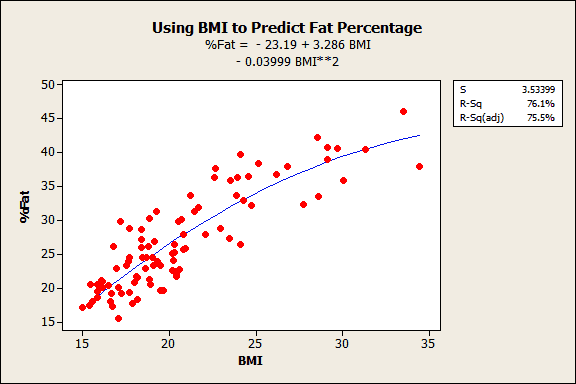
You’ll note the curved relationship, which is why I included the squared term. The fitted line follows the data very nicely because the observations fall randomly around it for the entire range. The R-squared is 76.1%, which isn't fantastic but not terrible. It reflects the imperfect nature of BMIs. We'll assess the residual plots below to really check the model. Remember, if the model isn’t a good fit, our predictions won’t be valid.
A side note about the implications of the curved relationship for the raw BMI scores of this population: We tend to think of BMI scores in a linear sense. That is, if you start at either 16 or 30 and increase BMI by 1, we assume that it represents the same increase in fat mass. The curved relationship shown above suggests that this is not true. The change in fat mass varies depending on the specific BMI value you start at. The overall effect is that raw BMI values tend to overestimate the fat mass for those with very low BMI scores and very high BMI scores. Middle-of-the-range BMI scores tend to underestimate fat mass. Regression analysis actually improves upon raw BMI scores for this population by correctly modeling the curvature. Yay Minitab!
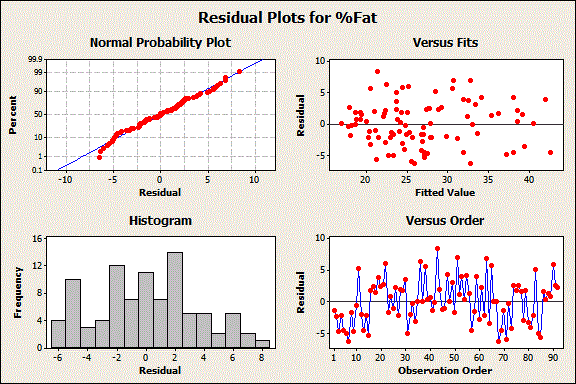
The residuals in the Normal Probability Plot above follow a straight line, which indicates they are normally distributed. In the Versus Fits plot, the residuals appear to be randomly scattered about zero. These data were not recorded in time-order so we can ignore the Versus Order plot. The histogram can help detect outliers, but none are evident. (Don’t use histograms to assess normality, because they can be deceptive for that purpose!)
Because the model is a good fit, we can start predicting. In part 2 of this series, we’ll generate predictions, assess accuracy, and compare Minitab's predictions to those of the BIA scales!


