In the world of linear models, a hierarchical model contains all lower-order terms that comprise the higher-order terms that also appear in the model. For example, a model that includes the interaction term A*B*C is hierarchical if it includes these terms: A, B, C, A*B, A*C, and B*C.
Fitting the correct regression model can be as much of an art as it is a science. Consequently, there's not always a best model that everyone agrees on. This uncertainty carries over to hierarchical models because statisticians disagree on their importance. Some think that you should always fit a hierarchical model whereas others will say it's okay to leave out insignificant lower-order terms in specific cases.
With Minitab Statistical Software, you have the flexibility to specify either a hierarchical or a non-hierarchical linear model for a variety analyses in regression, ANOVA, and designed experiments (DOE). In the example above, if A*B is not statistically significant, why would you include it in the model? Or, perhaps you’ve specified a non-hierarchical model, have seen this dialog box, and you aren’t sure what to do?
In this blog post, I’ll help you decide between fitting a hierarchical or a non-hierarchical regression model.
Practical Reasons to Fit a Hierarchical Linear Model
Reason 1: The terms are all statistically significant or theoretically important
This one is a no-brainer—if all the terms necessary to produce a hierarchical model are statistically significant, you should probably include all of them in the regression model. However, even when a lower-order term is not statistically significant, theoretical considerations and subject area knowledge can suggest that it is a relevant variable. In this case, you should probably still include that term and fit a hierarchical model.
If the interaction term A*B is statistically significant, it can be hard to imagine that the main effect of A is not theoretically relevant at all even if it is not statistically significant. Use your subject area knowledge to decide!
Reason 2: You standardized your continuous predictors or have a DOE model
If you standardize your continuous predictors, you should fit a hierarchical model so that Minitab can produce a regression equation in uncoded (or natural) units. When the equation is in natural units, it’s much easier to interpret the regression coefficients.
If you standardize the predictors and fit a non-hierarchical model, Minitab can only display the regression equation in coded units. For an equation in coded units, the coefficients reflect the coded values of the data rather than the natural values, which makes the interpretation more difficult.
You should always consider a hierarchical model for DOE models because they always use standardized predictors. Starting with Minitab 17, standardizing the continuous predictors is an option for other linear models.
Even if you aren’t using a DOE model, this reason probably applies to you more often than you realize in the context of hierarchical models. When your model contains interaction terms or polynomial terms, you have a great reason to standardize your predictors. These higher-order terms often cause high levels of multicollinearity, which can produce poorly estimated coefficients, cause the coefficients to switch signs, and sap the statistical power of the analysis. Standardizing the continuous predictors can reduce the multicollinearity and related problems that are caused by higher-order terms.
Read my blog post about multicollinearity, VIFs, and standardizing the continuous predictors.
Why You Might Not Want to Fit a Hierarchical Linear Model
Models that contain too many terms can be relatively imprecise and can have a lessened ability to predict the values of new observations.
Consequently, if the reasons to fit a hierarchical model do not apply to your scenario, you can consider removing lower-order terms if they are not statistically significant.
Discussion
In my view, the best time to fit a non-hierarchical regression model is when a hierarchical model forces you to include many terms that are not statistically significant. Your model might be more precise without these extra terms.
However, keep an eye on the VIFs to assess multicollinearity. VIFs greater than 5 indicate that multicollinearity might be causing problems. If the VIFs are high, you may want to standardize the predictors, which can tip the balance towards fitting a hierarchical model. On the other hand, removing the interaction terms that are not significant can also reduce the multicollinearity.
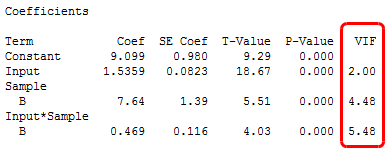
You can fit the hierarchical model with standardization first to determine which terms are significant. Then, fit a non-hierarchical model without standardization and check the VIFs to see if you can trust the coefficients and p-values. You should also check the residual plots to be sure that you aren't introducing a bias by removing the terms.
Keep in mind that some statisticians believe you should always fit a hierarchical model. Their rationale, as I understand it, is that a lower-order term provides more basic information about the shape of the response function and a higher-order term simply refines it. This approach has more of a theoretical basis than a mathematical basis. It is not problematic as long as you don’t include too many terms that are not statistically significant.
Unfortunately, there is not always a clear-cut answer to the question of whether you should fit a hierarchical model. I hope this post at least helps you sort through the relevant issues.


