I have a birthday coming up, and wanted to share a wealth of statistics about birthdays that you may find entertaining.
First is the "Birth Day Problem." Some of you probably encountered this one in a statistics class at some point. The Birthday Problem is as follows: How many people would need to be in a room in order for there to be a 50% chance that two share a birthday? This is a fun problem because the answer is surprising for many people. After all, we always seem surprised when we meet people we share a birthday with.
Often the answer you get is 183, or half of the number of days in most years (365). If you get 183 random people in a room and don't have two sharing a birthday, I'll send you $100.
For those more statistically-minded, you are probably thinking "Well, it's definitely lower than 183." But how low would you guess? 100? 50? Less?
The answer is 23.
So how is it so small? Well, we start by assuming every day is equally likely to occur, and ignoring Leap Days. That assumption is not 100% true, but as many have found (one example is here, including information on obtaining the data: http://chmullig.com/2012/06/births-by-day-of-year/), the assumption makes little difference compared to not making the assumption. The assumption also makes the math easier.
Then consider one person walking into a room. They have a unique birthday because they are the only person present. Then a second person walks into the room. There is a 364/365 chance that they also have a unique birthday. If they do, a third person walks into the room, who has a 363/365 chance of a unique birthday. This continues until someone enters with a matching birthday in the room. So to calculate the odds that we have a match, we take 1 minus the odds that all n people have unique birthdays or:
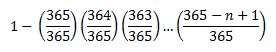
Curious about other odds? Here is a graph that should satisfy your curiosity:
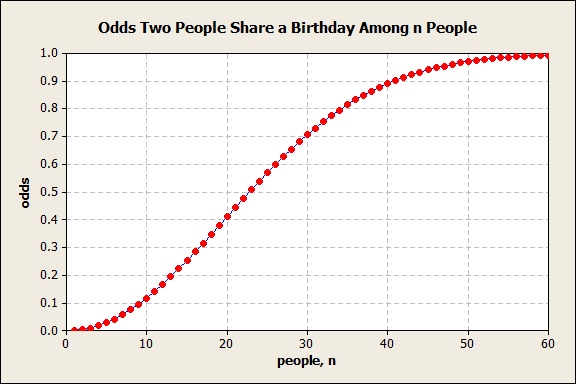
So there you have it, the odds of two people in a room sharing a birthday. But you don't get excited when you overhear a conversation between two people about them sharing a birthday. You want to meet someone who has YOUR birthday! In that case, we're now talking about sharing a specific day and the math is a little different.
Imagine you're alone in the room, and your birthday is December 12. Someone else walks in the room, and as before the odds that they have a "unique" birthday (not yours) is 364/365. A third person walks in. In the original problem, we needed them to have a birthday unique from the two people in the room so the odds were 363/365. But now you don't care if they share a birthday with the second person—heck, if they do then suddenly they are having a great conversation and you're the third wheel! So you only care about the odds that their birthday is not December 12, which again is 364/365. So now I am going to ignore you, and just say once n people have joined you the odds are:
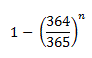
This subtle change in the equation has some big implications, and you shouldn't be surprised. After all, with 366 people in a room, we KNOW that two must share a birthday (ignoring the Leap Day). But in the same crowd we still might not have another December 12 birthday so we no longer have a bound. But go ahead and take a guess—how many other people do you think need to be in the room in order for there to be a 50% chance that one of them has your birthday?
50? More?
The answer is 253. Here is a full graph:
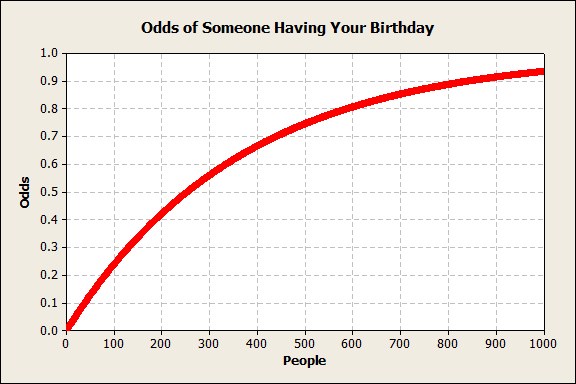
So the next time you're at a party, keep in mind that "Were you born on December 12?" (or your birthday) is not very likely to result in any interesting conversations.
Now that we got that out of the way, I'd like to change gears. My brother was born on November 1, so naturally as Halloween approached my mother was a bit nervous that she might have a Halloween baby. But could she—whether consciously or subconsciously—move the odds towards October 30 or November 1? Or rather than specific days, are babies just generally born more often during some parts of the year than others? Let's jump back to my previous statement that each day of the year does not have an equal proportion of births to other days.
It is surprisingly difficult to get a list of all birthdays, but I was able to get everyone born from 1969 through 1988. For statistical correctness, we'll just say that all further statstics are based only on those born during that period.
So here are the number of births for each day of the year during that period, with particular data points of interest labeled:
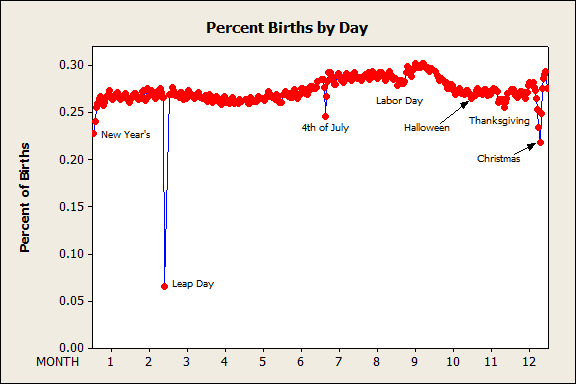
So it looks like although there may be some Halloween-baby fear out there, it does not make much difference in birth rate. However, we do have some other holidays that definitely see a reduced rate of births—specifically New Year's Day, the 4th of July, Labor Day (less pronounced because it is any one of seven dates), Thanksgiving (same effect type as Labor Day), and Christmas, along with some days around it. Leap Day also jumps out, but only because it only occurs every four years during this time frame: multiplying it by four to adjust for this causes it to no longer stand out.
Now, before anyone thinks that there are many women out there in Labor on Christmas Day that are refusing to go to the hospital until midnight, I should mention the very likely explanation for much of these effects. As due date approaches, there are a variety of reasons including health of the mom-to-be, health of the baby, and days past due that cause a doctor to go ahead and schedule a C-Section. Often the choice of day is not exact (except for emergency C-Sections) so there is some leeway—and in these cases, neither doctor nor patient are likely to want the appointment on a major holiday.
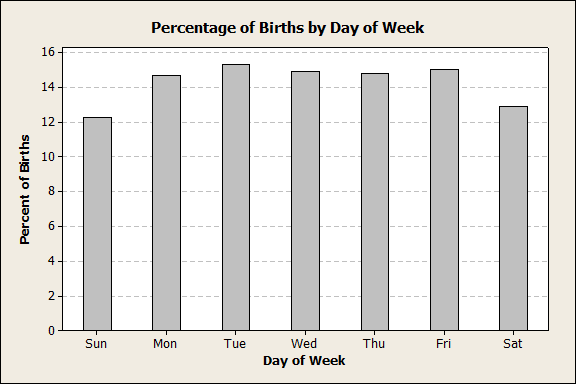
When else might a doctor not like to schedule a C-Section? A weekend! I know from recent experiences that weekend appointments typically are not even offered as an option. That too comes out in the data:
Now as anyone who has had a baby through natural delivery knows, the actual day the baby is born is highly variable around the due date, and certainly on the day you find out you are pregnant you don't already know the exact day the baby will be born. So next I want to look more generally at the broad trends throughout the year and smooth out individual days that may be unusual. And because I want to make things a little more interesting ( to me at least) I'm going to backdate the birth dates 266 days...the average human gestation period. Use your imagination for what this data might signify:
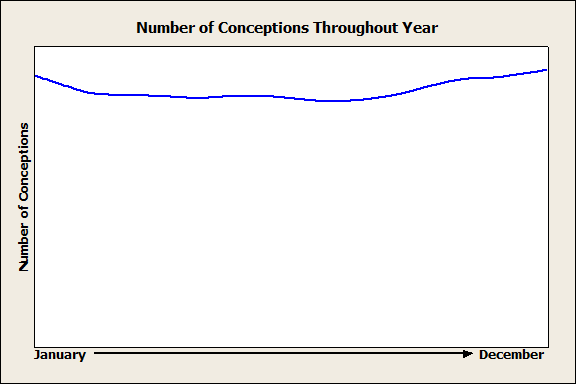
What is it about fall?


