In this post, I’ll address some common questions we’ve received in technical support about the difference between fitted and data means, where to find each option within Minitab, and how Minitab calculates each.
First, let’s look at some definitions. It’s useful to have an example, so I’ll be using the Light Output data set from Minitab’s Data Set Library, which includes a description of the sample data here. This same data set is available within Minitab by choosing File > Open Worksheet, clicking the Look in Minitab Sample Data folder button at the bottom, and then opening the file titled LightOutput_model.MTW.Calculating Data Means
In an ANOVA, data means are the raw response variable means for each factor/level combination.
For the LightOutput data set, we can calculate the data means for Temperature by choosing Stat > Basic Statistics > Display Descriptive Statistics, and then completing the dialog box as shown below:
Click the Statistics button and make sure only Mean is selected, then click OK in each dialog. Repeat the above steps, and replace Temperature with GlassType to calculate the data means for that second factor. The session window will display these results:
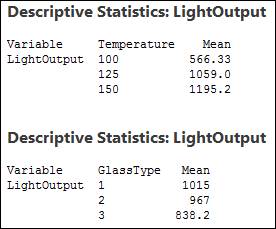
The means calculated directly from the data shown above are the values that would be plotted in a Main Effects plot. To create that plot in Minitab, use Stat > ANOVA > Main Effects Plot and complete the dialog box as shown below:
Click OK display the graph, which will show the same mean values for each level of the two factors (I’ve added data labels to the graph below):
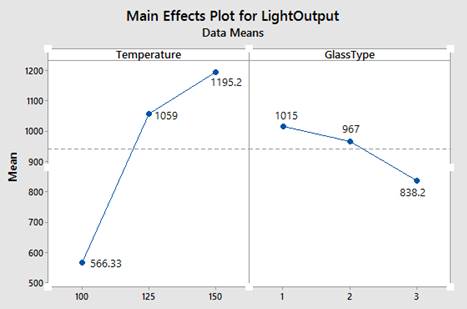
So, data means are the raw response variable means for each factor/level combination. On the other hand, fitted means use least squares regression to predict the mean response values of a balanced design, in which your data has the same number of observations for every combination of factor levels. The two types of means are identical for balanced designs but can be different for unbalanced designs.
Balanced Designs
As I mentioned above, in ANOVA a balanced design has an equal number of observations for all possible combinations of factor levels, whereas an unbalanced design has an unequal number of observations.
If you’re not sure whether your design is balanced or not, Minitab makes it easy to find out. For the Light output data set, we can see that the design is balanced by choosing Stat > Tables > Cross Tabulation and Chi-Square, and then completing the dialog as shown below:
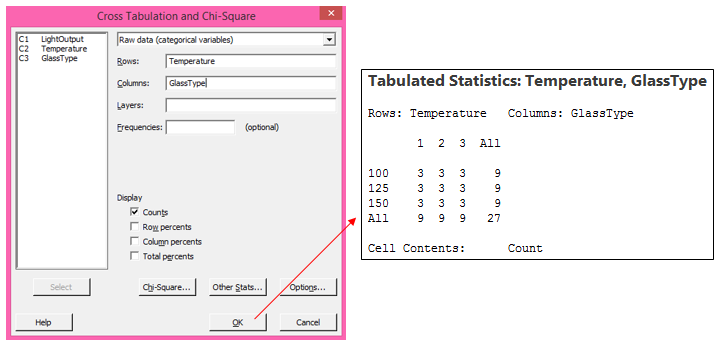
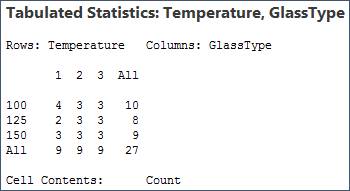
Because there are 3 observations for every combination of Temperature and GlassType, this design is balanced.
We can fit a model to this data by choosing Stat > ANOVA > General Linear Model > Fit General Linear Model, and then completing that dialog box as shown below and clicking OK:
Now that we have a model for this data, we can obtain a main effect plot based on the least-squares model by choosing Stat > ANOVA > General Linear Model > Factorial Plots (NOTE: The Factorial Plots option will not be available until a model is fit, because these graphs are based on the model). Click OK in the dialog box below to accept the defaults and generate the main effects plot:
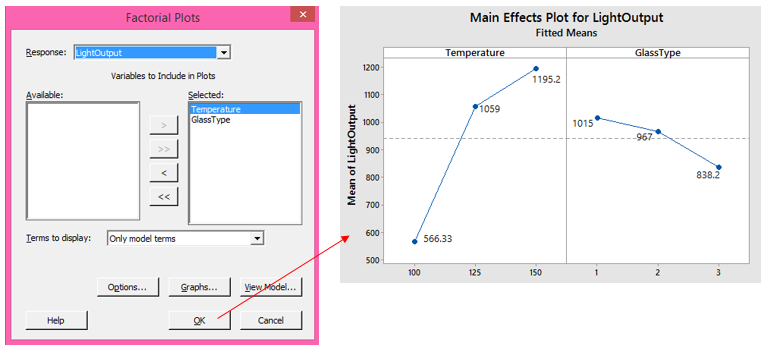
Calculating Main Effects for Balanced Designs
Again, the fitted means in the main effects plot above are the same as the previous data means plot because this is a balanced design. In this case, the answer is the same, but Minitab obtained these results by finding the fitted value for every possible combination of factor levels. The following steps illustrate what Minitab is doing automatically, behind the scenes:
-
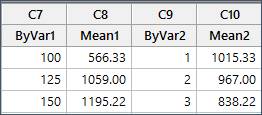
To obtain these fitted values, after the model has already been fit to the data, type all possible combinations of factor levels into the worksheet as shown below, and then use Stat > ANOVA > General Linear Model > Predict, and enter the two columns with all possible combinations:
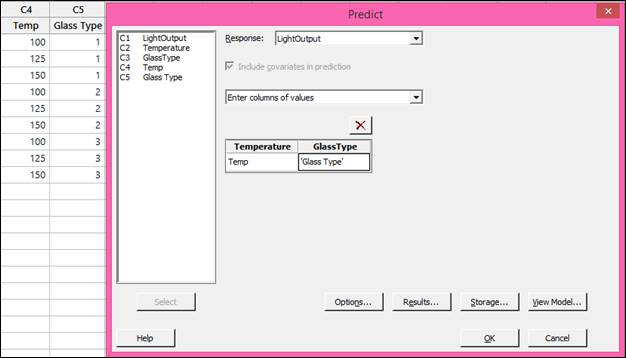
-
Click OK in the dialog box above to store the results in the worksheet.
-
Now use Stat > Basic Statistics > Store Descriptive Statistics twice; once to get the means of the fits calculated in step 2 for Temp, and a second time to get the means of the fits for Glass Type:
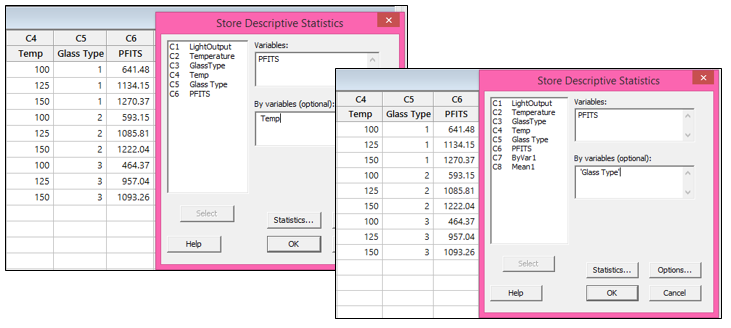
The results show the same means calculated in the fitted means main effects plot:
Unbalanced Designs
Now let’s take a look at what happens in an unbalanced design, where there are an unequal number of observations per factor/level combination.
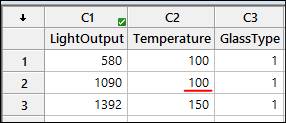
First, we’ll need to modify the worksheet to make the design unbalanced. Recall that this data set includes 3 observations per combination of factor levels. To make the design unbalanced, I’m changing the second row of data in the Temperature column. The original value there was 125, and I’ve changed that to 100:
With the data modified as shown above, we can use Stat > Tables > Cross Tabulation and Chi-Square again to see that the design is unbalanced:
Calculating Main Effects for Unbalanced Designs
Now let’s fit a model to this data using Stat > ANOVA > General Linear Model > Fit General Linear Model. This time, click the Results button and use the drop-down list next to Coefficients to select Full set of coefficients, then click OK in each dialog. Our results are different. If we generate new factorial plots using the new model, we can see that some of these fitted means are different than those in the balanced model:
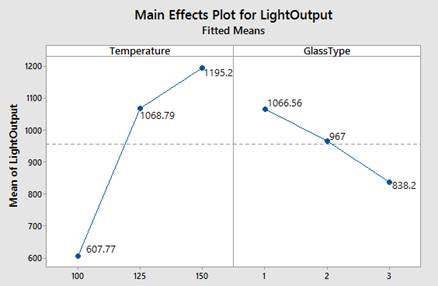
We can calculate the fitted means of the main effects in the same way as we calculated them for the balanced case, or we can see the same results by looking at the full table of coefficients:
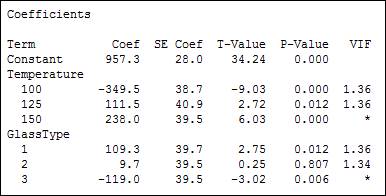
The fitted mean in the main effects plot for temperature at 100 is calculated by adding the coefficient for temperature at 100 to the constant. So 957.3 + (-349.5) = 607.8 (rounded). For temperature at 125, we add 957.3 + 111.5 = 1168.8, and so forth.
If you’ve enjoyed this post and would like to learn more, check out our other blog posts related to ANOVA.


