In our continuing effort to use experimental design to understand how to drive the golf ball the farthest off the tee, we have decided each golfer will perform half the possible combinations of high and low settings for each factor. But how many times should each golfer replicate their runs to produce a complete data set?
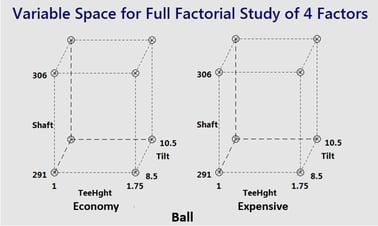 Well, last week we examined 5 reasons to use factorial experiments and concluded that our four factors – club face tilt, ball characteristics (economic vs. expensive), club shaft flexibility and tee height – could best be studied using all 16 combinations of the high and low settings for each – a full factorial.
Well, last week we examined 5 reasons to use factorial experiments and concluded that our four factors – club face tilt, ball characteristics (economic vs. expensive), club shaft flexibility and tee height – could best be studied using all 16 combinations of the high and low settings for each – a full factorial.
Each golfer’s data can stand as a complete half fractional study of our four research variables.
The data analysis for a DOE is multiple linear regression to produce an equation defining the response(s), as a function of the experimental factors. Run replicates serve four functions in this analysis:
- Higher replication produces more precise regression equation coefficients.
- Replicates are needed to estimate the error term for statistical tests on factor effects.
- Replicates allow the study of variation in our response.
- Replication provides replacement insurance against botched runs or measurements.
Measuring the variation at each run condition, log(standard deviation) is a common response, and allows the experimenter to study effects of the experimental factors on the response variation, in addition to the mean. This often leads to run conditions that reduce variability, which is almost a universal goal in manufacturing. Function 4 (above) just makes good sense. In fact, I always recommend at least two replicate runs so that one can be used as an outlier check against the other, as well as a replacement in case a true outlier is found.
Averaging Replicates and Variation
The first two functions above work together and require a power and sample size calculation to determine a reasonable estimate of the number of run replicates required to simultaneously meet both functions. Higher replications result in more precise estimates of the regression coefficients by averaging away the variation, according to the simple formula below:

This is illustrated in this diagram showing individual data compared to the same data, which has been grouped into samples of 4 and then averaged. The variation is reduced by a factor of sqrt(4) = 2.
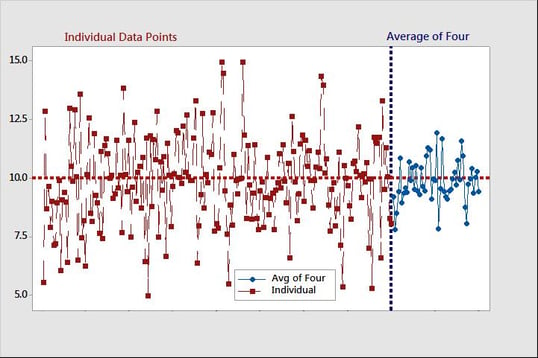
Averaging away variation allows you to detect effects despite the noise. This is taken to an extreme in a study which showed an effect of tee height by taking 27 random golfers and having them all drive 10 balls at each of 3 tee heights. All this just to study one variable! In DOE, it is best to take the opposite approach and control as many sources of variation as possible and minimize the number of replicates.
Power and Sample Size Calculations
The probability an experiment will detect a certain size effect on the response (power) depends on 4 factors:
- The size of the effect being estimated.
- The amount of variability in the data (standard deviation).
- Number of replications.
- Alpha = probability of type I error.
Using Minitab for our calculations, we set out to learn the number of replications required. The four golfers in our experiment estimated that their drives typically vary over a range of 50 – 60 yards. Assuming that this range of variability is about 5 – 6 standard deviations, we estimate our variability to replicate a drive is a standard deviation = 10 yards. Our calculation also requires an estimate from the golfers of the improvement in their drive distance that would result in an improved overall golf score. Their estimate was about 10 yards as well.
Finally, an effective data collection should have at least an 80% chance of detecting this ten-yard change if one of our factors does cause it. We enter this data into the power and sample size calculator in Minitab for a two-level factorial design and obtain the following results:
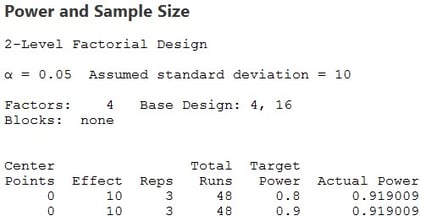
Each golfer would need to replicate the full 16 run factorial 3 times for a total of 48 runs if they expect the experiment to have a power of at least 80% or 90%, or actually about 92%. This is not an unreasonable value for one morning’s work for each golfer. On the other hand, if we planned on having the golfers only execute half of the full experiment for a total of 8 runs, our results would look like this:
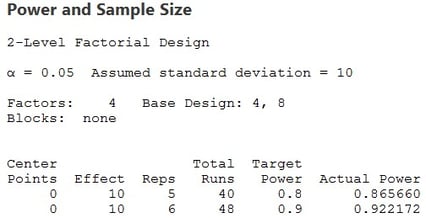
We could get away with 5 replications of the 8 run half fraction for a total of only 40 drives resulting in a power of about 87%. This is a good deal! We still have a reasonable power and 8 fewer drives per golfer.
Based on these results, we select 5 replications of the half fraction for each golfer as a sample size large enough to detect an effect large enough to impact our golfers’ final score.
A Final Note – Avoid a Standardized Effect Size
In the last calculation, we requested that our golfers estimate the range of variability in their drive and the size of the drive distance change that would have a significant impact on their golf score. These are two important requirements (standard deviation and effect size) for the calculation of the required replications.
Dr. Russ Lenth, a professor of statistics at the University of Iowa, discourages a common practice, which assumes a standard deviation = 1 and thus makes the effect size units of standard deviations (standardized effect). In an article on the subject, Some Practical Guidelines for Effective Sample Size Determination, he questions the value of knowing how many standard deviations of effect size we can detect if we don’t know the standard deviation. This does not allow the researcher to size the experiment so that it can detect the smallest level of change in the response that is large enough to have a business impact. This is what we are trying to do! I agree with Dr. Lenth on this point and, frankly, I am amazed at the number of times I see this not only approximate, but misleading, calculation carried out.
Your experiment is much better served by taking the time to estimate the standard deviation and determining the appropriate effect size when running these calculations.
So now we have our sample size. In our next post we will review the calculations for incorporating blocking variables and covariates in the analysis of the final data. See you at the driving range!
Many thanks to Toftrees Golf Resort and Tussey Mountain for use of their facilities to conduct our golf experiment.
Catch Up with the other Golf DOE Posts:
Part 1: A (Golf) Course in Design of Experiments
Part 2: 5 Reasons Factorial Experiments Are So Successful
Part 4: ANCOVA and Blocking: 2 Vital Parts to DOE
Part 5: Concluding Our Golf DOE: Time to Quantify, Understand and Optimize


