Like so many of us, I try to stay healthy by watching my weight. I thought it might be interesting to apply some statistical thinking to the idea of maintaining a healthy weight, and the central limit theorem could provide some particularly useful insights. I’ll start by making some simple (maybe even simplistic) assumptions about calorie intake and expenditure, and see where those lead. And then we can take a closer look at these assumptions to try to get a little closer to reality.
I should hasten to add that I’m not a dietitian—or any kind of health professional, for that matter. So take this discussion as an example of statistical thinking rather than a prescription for healthy living.
Some Basic Assumptions
Wearable fitness trackers like a FitBit or pedometer can give us data about the calories we burn, while a food journal or similar tool helps monitor how many calories we take in. The key assumption I am going to make for this discussion is that the number of calories I take in are roughly in balance with the calories I burn. Not that they balance exactly every day, but on average they tend to be in balance. Applying statistical thinking, I am going to assume my daily calorie balance is a random variable X with mean 0, which corresponds to perfect balance.
On days when I consume more calories than I burn, X is positive. On days when I burn more calories than I consume, X is negative. On a day when a coworker brings in doughnuts, X might be positive. On a day when I take a walk after dinner instead of watching TV, X might be negative. I will assume that when X is positive, the extra calories are stored as fat. On days when X is negative, I burn up stored fat to fuel my extra activity. I will assume each pound of body fat is the accumulation of 3500 extra calories.
The variation in X is represented by the variance, which is the mean squared deviation of X from its mean. The standard deviation is the square root of the variance. I will assume a standard deviation of 200 calories.
Each day there’s a new realization of X. If I assume each day’s X value is independent of that from the day before, then it’s like taking a random sample over time from the distribution of X. The central limit theorem assumes independence, so I’ll at least start off with that assumption. Later I’ll revisit my assumptions.
Based on all these assumptions, if I add up all the X’s over the next year (X1 + X2 + … + X365) that will tell me how much weight I will gain or lose. If the sum is positive, I gain at the rate of one pound for every 3500 calories. If the sum is negative, I lose at the same rate. So let’s apply some statistical theory to see what we can say about this sum.
First, the mean of the sum will be the sum of the means. That’s why I wanted to assume that my daily calorie balance has a mean of 0. Add up 365 zeroes, and you still have zero. Just like my daily calorie balance is a random variable with mean zero, so is my yearly calorie balance. So far so good!
Accounting for Variation
Next consider the variability. Variances also add. With the assumption of independence, the variance of the sum is the sum of the variances. I assumed a daily standard deviation of 200 calories, which is the square root of the variance, which would be 40,000 calories squared. It’s weird to talk about square calories, so that’s why I prefer to talk about the standard deviation, which is in units of calories. But standard deviations don’t sum nicely the way variances do. My yearly calorie balance will have a variance of 365 × 40,000 calories squared.
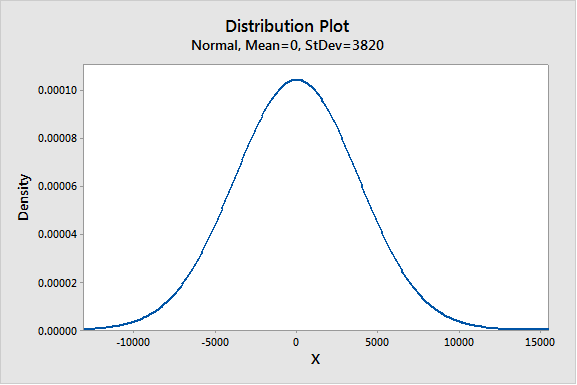
The standard deviation is the square root of this, or 200 times the square root of 365. The square root of 365 is about 19.1, so the standard deviation of my yearly calorie balance is about 19.1*200 = 3820. Is that good? Is that bad? Not sure, but this quantifies the intuitive but vague idea that my weight varies more from year to year than it does from day to day.
Enter the Central Limit Theorem
Now let’s bring the central limit theorem into the discussion. What can it add to what we have found already? The central limit theorem is about the distribution of the average of a large number of independent identically distributed random variables—such as our X. It says that for large enough samples, the average has an approximately normal distribution. And because the average is just the sum divided by the total number of Xs, which is 365 in our example, this also lets us use the normal distribution to get approximate probabilities for my weight change over the next year.
Let’s use Minitab’s Probability Distribution Plot to visualize this distribution. First let’s see the distribution of my yearly calorie balance using a mean of 0 and a standard deviation of 3820.
We can get the corresponding distribution in terms of pounds gained by dividing the mean and standard deviation by 3500.
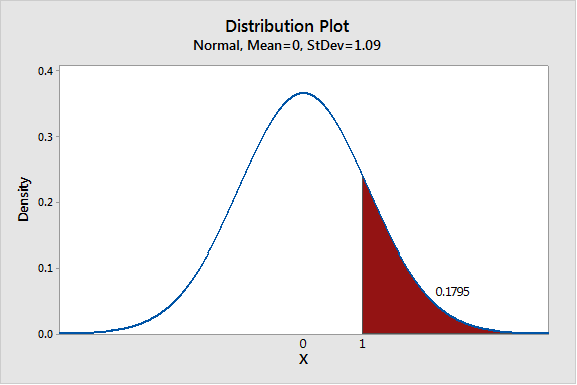
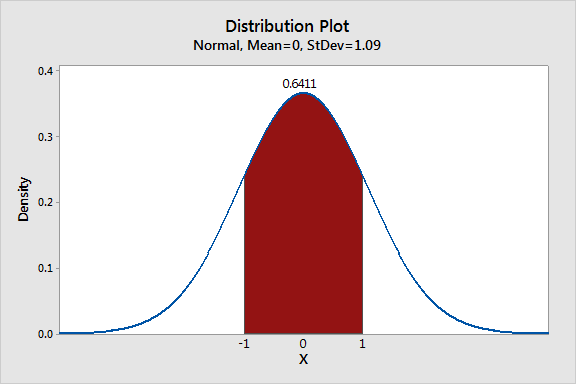
The right tail of the distribution is labeled to show that under my assumptions I have about an 18% probability of gaining at least one pound. The distribution is symmetric about zero, so I have the same probability of losing at least one pound over the year. On the bright side, I have about a 64% probability of staying within one pound of my current weight as shown in this next graph.
Before I revisit the assumptions, let’s project this process farther into the future. What does it imply for 10 years from now? What’s the distribution of the sum X1+X2+…+X3652 (I included a couple of leap years)? The mean will still be zero. The standard deviation will be 200 times the square root of 3652 or about 12,086. Dividing by 3500 pounds per calorie, we have a standard deviation of about 3.45. What’s the probability that I will have gained 5 pounds or more over the next 10 years?
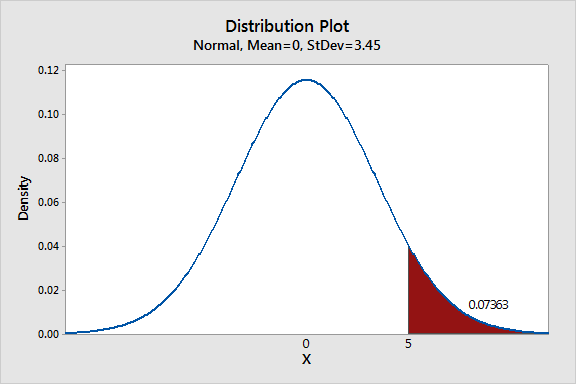
It’s about 7.3%. That’s actually not too bad!
A More Realistic Look at the Assumptions
Now let’s revisit the assumptions. A key assumption is that my mean calorie imbalance is exactly zero. I’m thinking that’s easier said than done—after all, I’m not weighing my food and calculating calories. I am wearing a smart watch to keep track of my exercise calories, but that’s only a piece of the puzzle, and even there, it’s probably not accurate down to the exact calorie.
So let’s look at what happens if I’m off by a little. Suppose the mean of X is slightly positive, say 10 calories more in than out per day. Means add up, so over a year, the mean imbalance is 365 ×10 = 3650 calories. So on average I’ll gain a little more than a pound. Applying the central limit theorem again, what’s my probability of gaining a pound or more in a year?
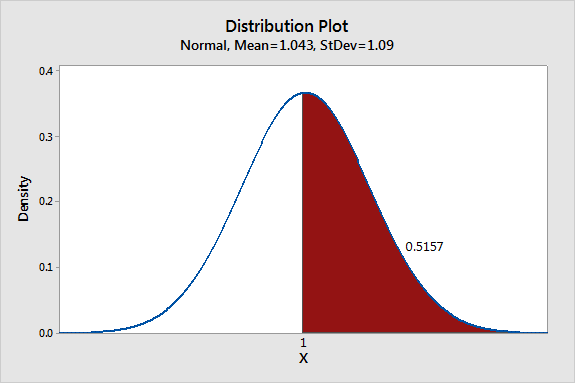
As this graph shows, the probability is about 51.57% that I will gain at least one pound in a year.
What about 10 years? The average is now 36,520 calories, which translates to about 10.43 pounds. Now what’s the probability of gaining at least 5 pounds over the next 10 years?
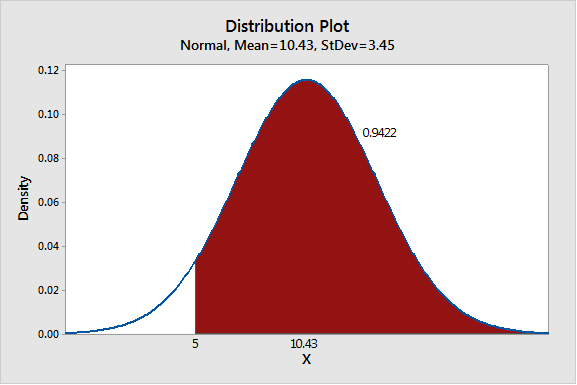
That’s a probability of over 94% of gaining at least 5 pounds, with gains of around 10 pounds or more being very likely.
That’s a big difference due to a seemingly insignificant 10 calorie imbalance per day. Ten calories is about a minute of jumping rope or a dill pickle.
Considering Correlation?
I assumed that each day’s calorie balance was independent of every other day’s. What happens if there are correlations between days? I could get some positive correlation if I buy a whole cheesecake and take a few days to eat it. Or if I go on a hiking trip over a long weekend. On the other hand, I could get some negative correlation if I try to make up for yesterday’s overeating by eating less or exercising more than usual today.
If there are correlations between days, then in addition to summing variances, I have to include a contribution for each pair of days that are correlated. Positive correlations make the variance of the sum larger, but negative correlations make the variance of the sum smaller. So introducing some negative correlations on a regular basis would help reduce the fluctuations of my weight from its mean. But as we’ve seen, that’s no substitute for keeping the long-term mean as close to zero as possible. If I notice my weight trending too quickly in one direction or the other, I had better make a permanent adjustment to how much I eat, how much activity I get, or both.


