In my experience, one of the hardest concepts for users to wrap their head around revolves around the Power and Sample Size menu in Minitab's statistical software, and more specifically, the field that asks for the "difference" or "difference to detect."
Let’s start with power. In statistics, the definition of power is the probability that you will correctly reject the null hypothesis when it is false. That’s a little abstract, so we can think of it a little more simply as the likelihood that you will find a significant effect or difference when one truly exists.
Let’s look at an example, and interpret the results. If we go to Stat > Power and Sample Size > 2 sample t, and enter the following:
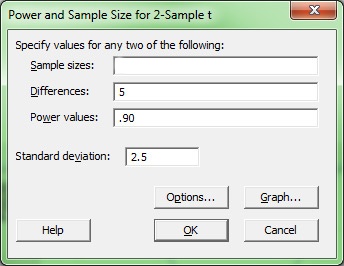
We get the following results:

What this tells us is the following: Assuming the standard deviation of our population is 2.5, and given that we want to achieve a power of 0.9, we would need a sample size of 7 to detect a difference in means of 5.
It’s a pretty straightforward idea that, all else being equal, the more samples you have, the more power you will have as well. But how does power relate to the “difference” a test can detect? If you play around in Minitab, you’ll find out how this affects power.
The first thing to be aware of is the link between sample size and the size of the difference you want to detect. In the 2-sample t dialog box shown above, this is what the "Differences" field is used for. The larger the difference you’re interested in, the smaller the sample size you would need to detect it.
A professor once offered me the following example, which I have found invaluable. Let’s imagine Michael Jordan gets together with LeBron James for some pickup basketball. They play a series of games until one player reaches 11 points. This would probably proceed with the two players alternating wins, until one person eventually pulled ahead. How many games would it take for you to determine who is a better player? Since the talent level is so similar, it would probably take a large number of games. Statistically, this is an example of trying to detect a very small difference. To detect a small difference, you need a much larger sample—in this case, games played—to achieve sufficient power.
Now, if Michael Jordan would play me in a pickup basketball game (a matchup with two players who do not have a similar talent level), it would take relatively few samples to realize that one player is better than another.
Hopefully, this provides a little more light on what Minitab is asking for in the “difference” field, and how potential changes in that affect your power and sample size calculations.


