Nala, our 6-year-old golden retriever, loves her dogma. That's her sitting in front of church on Sunday morning.
But she's not crazy about her catechism. For example, she doesn't always dutifully follow the "Lay Down" commandment.
What factors may be influencing her response? We're performing a DOE screening experiment to find out.
In this post, we'll use Minitab Statistical Software to
- Create the design for the experiment
- Determine the confounding pattern for this design
- Set up the data collection worksheet
Create the Design for the Experiment
In the previous post, we used the Display Design dialog box in Minitab to compare 2-level factorial designs for an experiment with 7 factors. Based on available resources, we decided to use a 1/8 fractional factorial design.
To create this design in Minitab, choose Stat > DOE > Factorial > Create Factorial Design. In Number of factors, enter 7. Click Designs and choose the 1/8 fraction design as shown below.
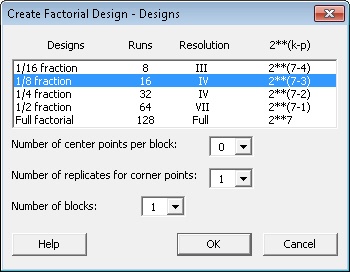
Click OK, then click Factors. Enter the name of each factor in the experiment, its type (numeric or text), and its low and high levels. Notice each separate factor is designated with a letter of the alphabet: A, B, C, D, and so on.
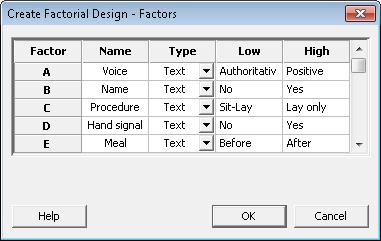
Click OK in each dialog box. Minitab will automatically do two things: Summarize the alias structure of your design and set up a randomized data collection worksheet for the experiment.
Understand the Alias Structure of Your Design
To see the summary of the design you just created, including its alias structure, look in the Minitab Session window (Tip: to make the Session window the active window, press Ctrl+M).
At the top, you'll see a summary of the number of factors, the number of runs, the type of factorial, its resolution, and other details of your design.
Fractional Factorial Design
Factors: 7 Base Design: 7, 16 Resolution: IV
Runs: 16 Replicates: 1 Fraction: 1/8
Blocks: 1 Center pts (total): 0
At the bottom, you'll see clumps of letters separated by plus signs.
Alias Structure
I + ABCE + ABFG + ACDG + ADEF + BCDF + BDEG + CEFG
A + BCE + BFG + CDG + DEF + ABCDF + ABDEG + ACEFG
B + ACE + AFG + CDF + DEG + ABCDG + ABDEF + BCEFG
C + ABE + ADG + BDF + EFG + ABCFG + ACDEF + BCDEG
D + ACG + AEF + BCF + BEG + ABCDE + ABDFG + CDEFG
E + ABC + ADF + BDG + CFG + ABEFG + ACDEG + BCDEF
F + ABG + ADE + BCD + CEG + ABCEF + ACDFG + BDEFG
G + ABF + ACD + BDE + CEF + ABCEG + ADEFG + BCDFG
AB + CE + FG + ACDF + ADEG + BCDG + BDEF + ABCEFG
AC + BE + DG + ABDF + AEFG + BCFG + CDEF + ABCDEG
AD + CG + EF + ABCF + ABEG + BCDE + BDFG + ACDEFG
AE + BC + DF + ABDG + ACFG + BEFG + CDEG + ABCDEF
AF + BG + DE + ABCD + ACEG + BCEF + CDFG + ABDEFG
AG + BF + CD + ABDE + ACEF + BCEG + DEFG + ABCDFG
BD + CF + EG + ABCG + ABEF + ACDE + ADFG + BCDEFG
ABD + ACF + AEG + BCG + BEF + CDE + DFG + ABCDEFG
The Alias Structure table can look a bit frightening at first glance. But this quasi "Scrabble board" in your output provides important information about your design.
Each row of the table shows you which effects and interactions in your experiment will be confounded with each other (that is, which effects you won't be able to tell apart) based on the design you've created.
For example, consider the first row of the main table body:
A + BCE + BFG + CDG + DEF + ABCDF + ABDEG + ACEFG
"A" represents the main effect for Factor A, which for this experiment is the tone of voice used to give the Lay Down command. Everything in this row will be confounded with main effect of A:
- The 3-way interactions BCE, BFG, CDG, DEF
- The 5-way interactions ABCDF, ABDEG, ACEFG
The interactions in this row will also be confounded with each other.
What does this mean, in concrete terms? A is in the same row as DEF. Therefore, I won't be able to discriminate between the effect of the tone of voice (A) with the interaction between the hand signal (D), the location (E), and the reward used (F).
This confounding is the "sacrifice" I made when I chose the 1/8 fractional design, with its lower resolution, to reduce the number of runs in my experiment.
If I had created a full factorial design with these 7 factors, there wouldn't even be an aliasing table in the design summary, because all the effects could be estimated separately:
Full Factorial Design
Factors: 7 Base Design: 7, 128
Runs: 128 Replicates: 1
Blocks: 1 Center pts (total): 0
All terms are free from aliasing.
If the alias table shows that potentially important interactions in your experiment are confounded, you may want to create a different design with a higher resolution before you start collecting data.
For this rough screening experiment, my main concern was that the 2-way interactions would not be confounded with the main effects. You can verify that this is the case by looking at the rows in the alias table: None of the rows that contain main effects (A B C D E F G) contain any 2-way interactions (AB AC AD and so on). Therefore, main effects and 2-way interactions can be estimated separately.
Note: Many of the 2-way interactions are confounded with each other--that could affect the interpretation of the results.
View the Data Collection Worksheet
To see the data collection worksheet for the experiment, look in the Data window. (Tip: to make the Data window the active window, press Ctrl+D).
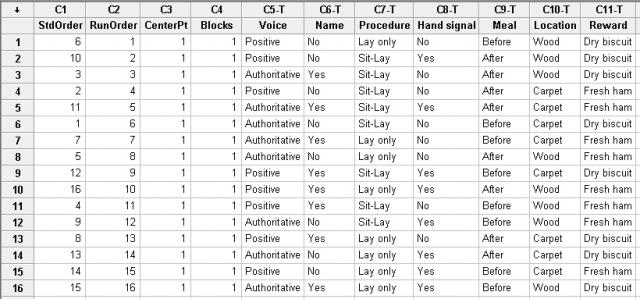
Minitab automatically randomizes the run order to prevent experimental bias, such as possible time-dependent effects. The random order is given by the RunOrder column (C2). The StdOrder column indicates the conventional order of the runs if they are not randomized.
Add a Label for the Response Column
Use the next available empty column for the response data. In this example, I've labeled column c12 Response.

As you perform the experiment, just follow the run order in the worksheet and record the measured response for each run.
In this experiment, I'll record the number of seconds (to the nearest hundredth of a second) that it takes Nala to lay down after being given the command.
Next Time...the Finale
Will the sweet aroma of honey-cured ham inspire Nala to bring her belly to the floor? And will adding the "cush factor" (carpeting) make her lay down even more quickly?
Find out in the next post....


