Recap: Lionel Loosefit has been arrested and hauled to court for violating the assumptions of regression analysis. In the previous court session, the prosecution presented evidence to show that the errors in Mr. Loosefit’s model were not normally distributed. Today, the prosecution addresses the second alleged violation: namely, that the errors in the defendant’s regression model are not independent. Dr. Minnie Tabber, a world-renowned statistician, is on the witness stand.
Prosecutor: Let me remind the members of the jury that a residual is simply the difference between the data value estimated by the regression model and the actual observed data value. Now, the law clearly states that besides being normally distributed, residuals should be independent. Why is that so important, Dr. Tabber?
Dr. Tabber: If the assumption of independence is violated, some model-fitting results may be questionable. For example, a positive correlation between error terms can inflate the t-values for coefficients.
Prosecutor: Inflated t-values. That sounds rather serious.
Dr. Tabber. It can be. An inflated t-value can make predictors in a model appear to be significant when they’re really not.
Prosecutor: So an unsuspecting victim might be led to think they’ve found a statistically significant association between variables, but really it’s just a fluke, an illusion...a shadow puppet show of p-values, as it were.
Dr. Tabber: Umm, something like that.
Prosecutor: Still, this all sounds a bit abstract to most of us. Is there any practical way an average person without statistical background can quickly check the independence of the residual errors?
Dr. Tabber. Yes, using a plot of the residuals vs the order of observations in Minitab. The plot provides a quick, practical means of visually examining residuals for potential correlation.
Prosecutor: Your honor, I’d like to present Exhibit E, a residuals vs order plot from the defendant’s regression model. But before doing so, I must warn our spectators in the courtroom that these Minitab results are extremely graphic.
[Hushed murmurs.]
Judge: Those with delicate constitutions may leave the courtroom.
[Stenographer gets up and exits.]
Judge: All right, let’s see the evidence, counselor.
Prosecutor: Ladies and gentlemen, I give you Exhibit E.
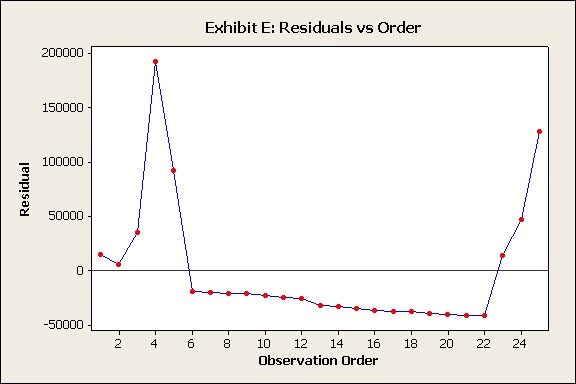
[Spectator stands, screams, swoons, and faints.]
Judge: Is there a medic in the house? Bailiff, please assist this unfortunate person.
Prosecutor: These kinds of things are never easy to see, are they Dr. Tabber?
Dr Tabber [shuddering]: No. Not even after years in the field.
Prosecutor: So tell us...would you call these residual errors random and independent?
Dr. Tabber: No, not at all. When errors are random and independent, you expect to see the points on the plot “bounce up and down” haphazardly at various heights on both sides of the 0 axis line. But here, there’s a clear pattern—a long sequence of negative residuals from observations 6 to 22.
Prosecutor: What, pray tell, does this ominous pattern portend?
Dr. Tabber: Well, residuals that cluster on the same sign—that is, either on the positive or the negative side of the 0-axis—often indicate a positive correlation.
Prosecutor: What might cause this insidious correlation, Dr. Tabber? What is shackling these residuals and preventing them from being truly independent, truly free?
Dr. Tabber: Not being familiar with the specifics of this experiment, I can’t really say. It could be something related to the experimental conditions...or the measuring instruments...or even data recording errors. Any number of things.
Prosecutor: Thank you, doctor. That’s all for now.
The Cross-Examination: Does the State Lack Hard Evidence?
Judge [to defense attorney]: You may cross-examine the witness.
Defense Attorney: Dr. Tabber, that plot of residuals vs. order is certainly a dramatic visual, isn’t it? It really gets the attention of our spectators.
Dr. Tabber: Graphic analyses in Minitab often do that.
Defense Attorney: Yes, of course. But isn’t it true, Dr. Tabber, that the plot doesn’t provide a formal statistical assessment of autocorrelation? In reality, isn’t it just a rough way to eyeball whether there may appear to be an association between the residuals and the order of the observations?
Dr. Tabber: Technically that’s true. Still, the plot is an extremely useful tool. If there’s nothing amiss on the plot, you can usually safely assume that the assumption of independence is satisfied.
Defense Attorney: Yes, yes, we understand all that. But isn’t true, Dr. Tabber, that there exists a more formal, definitive way to assess autocorrelation of the residuals in a linear regression model?
Dr. Tabber [stiffening]: Certainly. One can formally evaluate the presence of autocorrelation of the residuals using the Durbin-Watson statistic.
Defense Attorney: The Durbin-Watson statistic. What a lovely name. Yet this sublime value was never calculated by the State on Mr. Loosefit’s residuals, was it?
Dr. Tabber: Not that I’m aware of.
Defense Attorney: Why do you think that is?
Dr. Tabber: Well, a lot of people don’t know about the test. You’d need to use Stat > Regression > General Regression in Minitab, the most versatile linear regression command. The statistic is not displayed by default. So you need to click Results, and check Durbin-Watson statistic.
Defense Attorney: As shown in this Minitab subdialog box?
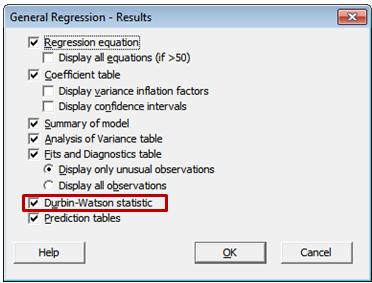
Dr. Tabber: Yes.
Defense Attorney: So you just check that box and click OK and that’s it? That seems pretty straightforward.
Dr. Tabber: Well, it’s not that simple. The interpretation is bit technical. To reach a conclusion from the test, you need to compare the displayed D-W statistic with lower and upper bounds in a statistical table. The bounds depend on the number of predictors in your model and the alpha level you’re using. If D-W is greater than the upper bound, no correlation exists; if D-W is less than the lower bound, positive correlation exists. If D-W is in between the two bounds, the test is inconclusive.
Defense Attorney: Be that as it may, the State never even bothered to perform the test. Hmmmm. What a pity. No further questions, your honor.
Judge: Dr. Tabber, you may be seated.
A Surprise Witness Takes the Stand
Prosecutor: Your honor, we’d like to call our next witness to the stand.
Judge: Proceed.
Prosecutor: The State calls Mr. Elmer Fudd, machine maintenance specialist at the defendant’s workplace.
Defense Attorney: Objection your honor! We did not expect to cross-examine a cartoon character! We request a temporary adjournment to prepare for this.
Judge: Denied. Mr. Fudd, please take the stand.
[Elmer Fudd enters the witness box and is sworn in.]
Prosecutor: Mr. Fudd, you are employed as a machine maintenance specialist at Mr. Loosefit’s workplace, is that correct?
Mr. Fudd: Cowwect.
Prosecutor: And you service the machine that Mr. Loosefit uses to measure his response data. What kind of machine is that?
Mr. Fudd: A wireless widget wedge wotater.
Prosecutor: Precisely. Every company has one. Now, you’ve just seen the residuals vs order plot and the striking pattern of correlation in observations 6 through 22. Can you tell us—about the time that this data was collected, did you get a call to service the machine?
Mr. Fudd: Yes.
Prosecutor: And what did you find?
Mr. Fudd: A wittle thing was stuck in the wotater. It alweady smelled wotten.
Prosecutor: Aha. Something was stuck in the rotater. And you removed the object, didn’t you? What exactly was it?
Mr. Fudd: It wooked like a wittle wabbit. But it was wed. And wubbewy.
Prosecutor: Let me get this straight. Are you telling the court that a wittle, wed, wotten, wubbewy wabbit was stuck in Mr. Woosefit’s wireless widget wedge wotater?
Defense Attorney: Objection your honor! The very idea of a rabbit getting stuck in a rotater is simply preposterous. This witness is a Looney Tune.
Judge: Ovewwuled!
Prosecutor: We agree it sounds preposterous, your honor. But only because Mr. Fudd thought this tiny, colorful object stuck in the machine resembled a small rabbit. Mr. Fudd, do recognize this?
Mr. Fudd: Thaiw he iz!!! That danged wabbit!
Prosecutor: Not a rabbit, Mr. Fudd, but a bear. A gummi bear, to be precise. Which, stuck in any wireless wedge rotater over time, produces a powerful alloy of citric acid, glucose syrup, and gelatinous prions, which causes the vertical feed handwheel behind the column saddle of the locking lever to stick against the gibhead key, triggering a consistency backlash on the y-axis locks that control the magnetic agitator for the hydraulic friction clutch in the hydro-extractor. And we all know what that leads to, don’t we? Progressive high-frequency belt creep on the driving face of the pneumatic prong of the grubscrew pully! Hence, the sequence of correlated residuals!
Lionel Loosefit [jumps up]: HE'S LYING! I DON’T EVEN LIKE GUMMI BEARS! THEY GET STUCK IN MY TEETH!
Judge: Order! Mr. Loosefit, another outburst like that and I’ll have you forcibly removed.
Prosecutor: You may or may not like gummi bears, Mr. Loosefit. That’s beside the point. Because we’ve discovered that an esteemed colleague of yours has been conducting an elaborate set of designed experiments on gummi bears for many months now, including a novel catapault experiment that is likely to have launched this red gummi bear directly into your rotater.
Lionel Loosefit [jumps up again]: No. NO! It’s not true. You’re using these graphs to plot against me!
Judge: We’ve heard enough for one day. Bailiff, take Mr. Loosefit away.
Judge: Is there a medic in the house? Bailiff, please assist this unfortunate person.
Judge: Is there a medic in the house? Bailiff, please assist this unfortunate person.
Judge: Is there a medic in the house? Bailiff, please assist this unfortunate person.