New to confidence intervals? Here are some important things to keep in mind!
Confidence Intervals:
- are used to estimate population parameters (commonly the process mean, standard deviation, % of defective units, or even capability indices).
- provide more meaningful information than any random sample statistic for characterizing the population.
MINI-TIP:
See “Tip 1: Every sample statistic is a little bit wrong.”
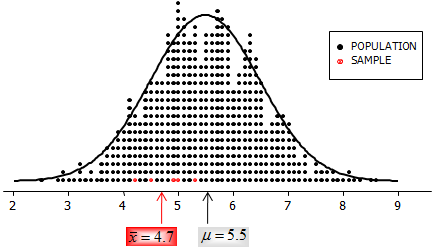
When your 95% confidence interval for the mean is (μlow, μhigh), you can be 95% confident that the population (process) mean, μ, is between μlow and μhigh …and 5% confident that μ is not between μlow and μhigh.
When your 95% confidence interval for the standard deviation is (σlow, σhigh), you can be 95% confident that the population standard deviation, σ, is between σlow and σhigh …and 5% confident that s is not between σlow and σhigh.
MINI-TIPS:
Multiply the high estimate for σ by 6 to approximate the potential range of a normal distribution. Multiplying the sample standard deviation, σ, by 6 tells us nothing about the population.
When your 95% confidence interval for the proportion of defectives is (plow, phigh), you can be 95% confident that the process is producing at least plow x100% defectives, and potentially as many as phigh x100% defective units.
For example, suppose you inspect 100 units and find 2 defectives. The sample % defective is 2%. But, using Minitab's 1 Proportion study, we create the 95% confidence interval for the proportion of defectives: (0.0024, 0.070). So this sample may be from a process that is producing a whopping 7% defective units!
TAKE-AWAY PERSPECTIVE:
There is always some RISK that even the confidence intervals will not contain the parameter of interest. That said, just imagine how risky it is to assume any sample statistic adequately characterizes the population!
More Facts About Confidence Intervals:
- INCREASING the % confidence INCREASES the length of the interval.
- INCREASING the sample size DECREASES the length of the interval.
MINI-TIP:
Use Minitab’s ‘Power and Sample Size for Estimation’ to determine sample sizes necessary to create confidence intervals of meaningful length.
- INCREASING the sample size does not increase the likelihood that the interval will contain the population parameter. Only increasing % confidence does this.
TAKE-AWAY PERSPECTIVE:
Confidence intervals based on small samples are as credible (reliable) as those based on large samples.
- The true population parameter may be near one end of the confidence interval.
TAKE-AWAY PERSPECTIVE:
Do not assume that the parameter of interest is near the middle of the interval.
- A 95% Confidence Interval DOES NOT contain 95% of the individual values in the population.
MINI-TIP:
Use Minitab’s ‘Tolerance Intervals’ to create intervals that capture a desired percent of the individual population values, with a given degree of confidence.
In Tip 4, we'll provide a brief explanation of tolerance intervals.
To gain more perspectives on statistical analysis procedures using Minitab Statistical Software, visit Minitab's web site for course descriptions and training opportunities, both public and on-site, at http://www.minitab.com/en-us/services/training/


