In my previous post, I shared a case study of how a small bicycle-chain manufacturing company in India used the DMAIC approach to Six Sigma to reverse declining productivity.
After completing the Define, Measure, and Analysis phases, the team had identified the important factors in the bushing creation process. Armed with this knowledge, they were now ready to make some improvements.
The Improve Phase
In the Improve phase, the team applied a statistical method called Design of Experiments (DOE) to optimize the important factors they'd identified in the initial phases.
Most of us learn in school that to study the effects of a factor on a response, you hold all other factors constant and change the one you're interested in. But DOE lets you change more than a single variable at a time. This minimizes the number of experimental runs necessary to get meaningful results, so you can reach conclusions about multiple factors efficiently and cost-effectively.
DOE has a reputation for being difficult, but statistical software makes it very accessible. In Minitab, you just select Stat > DOE > Create Factorial Design..., select the number of factors you want to study, then choose from available designs based on your time and budget constraints.
In this case, the project team used Minitab to design a 2x2 experiment, one that had two levels for each of the two factors under examination. They did two replicates of the experiment, for a total of eight runs. The experimental design, and the measured diameter (the response) for each run is shown below in the data sheet below:
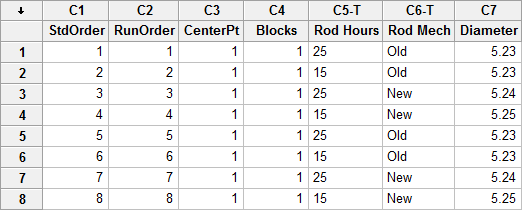
Once they'd collected the data, the team used Minitab to create plots of the main effects of both factors.
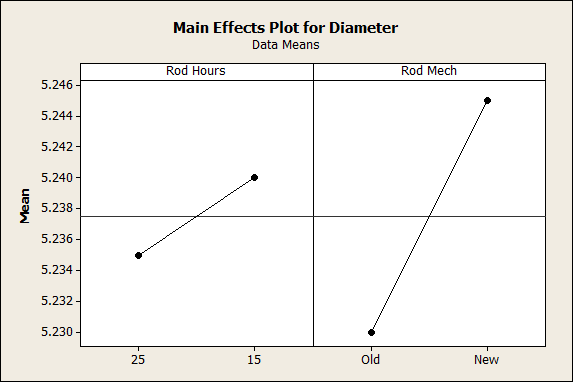
The slope of the lines on the main effects indicates how large an effect the factor has on the response: the steeper the slope, the greater the impact. The main effect plots above indicates that replacing the rod at 15 hours has a minor effect, while using a new rod-holding mechanism has a greater effect.
The team also created an interaction plot that showed how both factors worked together on the response variable:
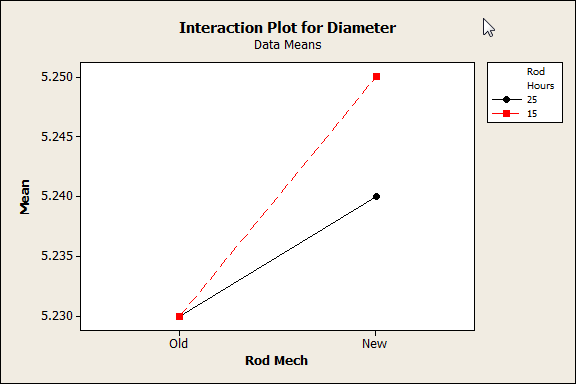
Parallel lines on an interaction plot indicate that no interaction between factors is present. Since the lines in this plot intersect, there is an interaction. As the research team put it in their paper, this means "the change in the response mean from the low to the high level of rod replacement depends on the level of rod-holding mechanism."
These analyses enabled the team to identify the important factors in creating bushings that fit inside the required limits, and indicated where they could adjust those factors to improve the manufacturing process.
The Control Phase
Once the team's recommended improvements had been implemented, it was time to gather data about the new process and assess whether it had made a difference in the bushing rejection rate.
The team again collected 20 subgroups of 5 samples each (n=100) from bushings created using the improved process. (Once again, we have used simulated data that match the parameters of the team's actual data, so the results are extremely similar but not completely identical to those shown in the original report.) The results of the capability analysis are shown below:
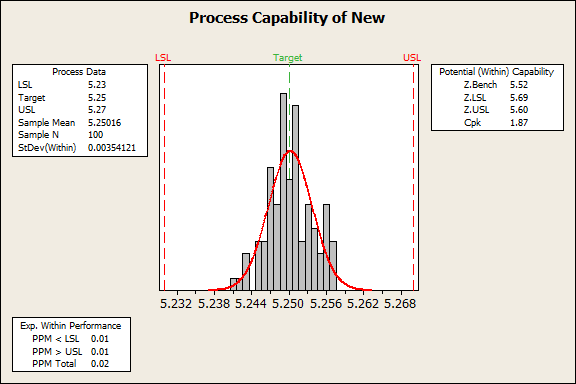
The PPM -- the number of defects per million opportunities -- fell to 0.02, while the Z.Bench or Sigma capability score reached 5.52. That's a tremendous improvement over the original process's 8% rejection rate and 1.4 Z.bench score!
That's not quite the end of the story, though: the Control phase doesn't really end, because the owner of the process that's been improved needs to ensure that the improvements are sustained. To do this, the organization used X-bar R control charts to ensure that the improved process remained on track.
Six Sigma Project Results
So, did this project have a positive impact on the bottom line of this small manufacturing enterprise? You bet. Implementing the team's recommendations made this a 5.5-sigma process, and improved the Application of project recommendation brought up the sigma level to 5.46 and reduced the monthly bushing rejection rate by more than 80,000 PPM.
That worked out to a cost savings of about $120,000 per year. For a business of any size, that's a significant result.
Visit our case studies page for more examples of how different types of organizations have benefit from quality improvement projects that involve data analysis.


