Definitive Screening Designs (DSDs) are a new class of Designs of Experiments (DoE) that have generated a lot of interest for product and process optimization. They are available in Minitab Statistical Software.
Traditionally, several types of designs of experiments have been available for practitioners to optimize processes and products:
-
Screening designs, to identify the few really significant factors out of a very large number of potential candidates
-
Factorial 2k designs, to study interactions in addition to main effects and build more comprehensive models
-
Response surface designs to describe quadratic effects and identify optimal settings
Definitive Screening Designs share many characteristics with these three very different classes of DoEs.
Response Surface Designs
Definitive Screening Designs are three level designs that enable one to study second order, quadratic effects. However, with only one center point and a number of runs that is much smaller than in a standard response surface design, the probability to detect significant quadratic terms (the power level) is certainly not as high.
Screening Designs
DSDs can also be considered as screening designs, since the number of terms to estimate in a full quadratic model, for example, is usually much larger than the number of tests. Traditional, Plackett Burman screening designs enable one to study main effects only, whereas Definitive Screening Designs can be used to study the effects of main effects as well as two factor interactions and quadratic effects.
Fractional Factorial Designs
Unlike fractional factorial designs in which some terms are fully confounded, Definitive Screening Designs provide estimates of two factor interactions with partial confounding. Interactions are also partially confounded with quadratic terms. In a DSD, however, all main effects are clear of any alias (not confounded with any other term) just like resolution IV fractional designs (learn more about resolutions in factorial designs here).
DSDs may therefore be considered as a multipurpose type of DoE, they are definitive in the sense that they provide an exhaustive, all-purpose, final solution to designing experiments.
Structure of a Definitive Screening Designs Array
Consider the structure of a DSD array, below.
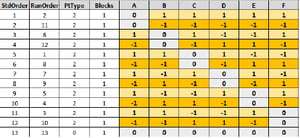
Design table of a thirteen runs DSD array for six factors
Center and Axial Points
Note that the last row of the DSD array above, is clearly a center point (all 0 settings for all factors), while all other rows contain one single 0 value (diagonal of the array). In a response surface design, the rows with one 0 setting would be considered as axial (star) points. This three levels design enables one to study quadratic effects.
With a single center point, only quadratic effects that are strong enough will become noticeable. Anyway, if the objective is to identify the optimum, the experimenter is likely to be interested only in large curvatures that markedly differ from a simple linear model.

Definitive Screening Designs: Coverage of the experimental space
Folded Over Pair of Rows
Consider the first two rows of the array, the second row is a mirror (folded over) image of the first row (with all signs systematically changed). This is based on a well known technique to convert a screening design into a resolution IV factorial design (so that all main effects are clear of any alias).
In a resolution III fractional factorial design, for example, two factor interactions are (fully) aliased with main effect factors, but if one replicates the initial screening design, with all signs systematically changed (folded over) and then assembles the initial screening fraction together with the folded over fraction, the result is a resolution IV factorial design in which confoundings between main effects and two factor interactions are resolved. Likewise, all rows within this DSD array (except for the center points) are a pairwise mirror image of another row.
Thanks to that, no two factors interaction will be aliased with any main effect in a DSD, although two factor interactions are (partially) confounded with one another. In DSDs, second order effects are also partially confounded with two factor interactions and with one another, but main effects are protected against any confounding.
In a 13 runs, 6 factors DSD, for example:
-
Correlations between two factor interactions range from ±0.25 to ±0.5 (partial confounding)
-
Factorial 2k designs, to study interactions in addition to main effects and build more comprehensive models
-
With 0.133 correlations between quadratic effects
-
Correlations between interactions and quadratic effects equal to either 0 or ±0.465
Why Definitive Screening Designs can be considered to be definitive designs
The traditional approach to designing experiments is to start with a screening design to screen out the important main effects, then transform this screening design into a resolution IV design to study the interactions.
This can be done by either folding over the initial screening design or due to the “projective” properties of screening designs, one may realize that after having reduced the number of terms to the ones that are statistically significant only, the screening design may be “projected” into a full 2k design (with some replicates). Sometimes, all the tests that are needed for a full factorial design are already in the screening design, so that no additional experiments will be needed.
Finally, by adding some axial and center points, this design can be converted into a response surface design.
DSDs do all of this in a single step, in that sense they are definitive.
Analysis of the results from a Definitive Screening Design
Due to the very large number of potential terms in a full quadratic model (main effects plus two factor interactions plus quadratic effects, with more terms than runs) no degrees of freedom are usually left to estimate the error term. DSDs are often fully saturated designs so that a stepwise regression is required at the analysis stage (see the suggestion below displayed in Minitab).
Consider running the analysis with a stepwise procedure to help identify important terms.
DSD designs, are based on the “sparsity” principle. We expect that, out of a very large number of potential terms, only few among them will eventually turn out to be really significant.
Conclusion
DSDs may be considered as a multipurpose, very flexible type of DoE. Of course, compared to dedicated response surface designs, the power level to detect quadratic effect is certainly much lower. In that respect, DSDs might appear to be a less expensive alternative to Central Composite or Box-Behnken designs, with a much smaller amount of runs, only one center point and obviously much less power.
The analysis stage is more complex than in standard factorial DOEs, since DSDs are often fully saturated designs and interactions as well as quadratic terms are partially confounded. They tend to work well when the “sparsity” principle applies, with an underlying model that is not too complex when compared to the very large number of initial candidate terms.
Check our Support pages to discover more about Definitive Screening Designs or attend our Training courses to learn the available designs in Minitab Statistical Software and select the right one for your project, check our DOE in practice course description.


