Äquivalenztests für die Qualitätsanalyse (Teil II): Welchen Unterschied macht die Differenz?

In vorausgegangenen Beitrag habe ich erläutert, wie Sie die Beweislast bei einem Hypothesentest des Mittelwerts mit einem Äquivalenztest umkehren. Damit können Sie besser testen, ob der Prozessmittelwert gleich einem Sollwert oder einem anderen Mittelwert ist.

Hier ist ein weiterer wichtiger Unterschied: Zum Durchführen eines Äquivalenztests müssen Sie vorab festlegen, wie groß die praktisch wichtige Differenz zwischen dem Mittelwert und dem Sollwert bzw. zwischen zwei Mittelwerten ist.

Ehrlich gesagt, sollten Sie den Wert dieser Differenz auch bei regulären Hypothesentests wissen. Denn ohne ihn können Sie nicht auswerten, ob Ihre Analyse eine hinreichende Trennschärfe aufweist. Außerdem können Sie nicht auswerten, ob eine statistisch signifikante Differenz in Ihren Testergebnissen auch in der realen Welt außerhalb der Theorie der Wahrscheinlichkeitsverteilungen bedeutsam ist.

Da Sie diese Differenz für einen regulären t-Test jedoch nicht festlegen müssen, wird dieser Test häufig mit einer nur vagen Idee dessen durchgeführt, was festgestellt werden soll. Eigentlich ist dies kein Fehler. Es ist eher so, als ob Sie ein Radon-Messgerät benutzen, ohne zu wissen, welche Radon-Pegel potenziell gefährlich sind.

ÄQUIVALENZGRENZEN FESTLEGEN: HIER SIND SIE GEFRAGT

Wie nahe muss der Mittelwert am Sollwert oder einem anderen Mittelwert liegen, damit Sie diese in der Praxis als „äquivalent“ bezeichnen?

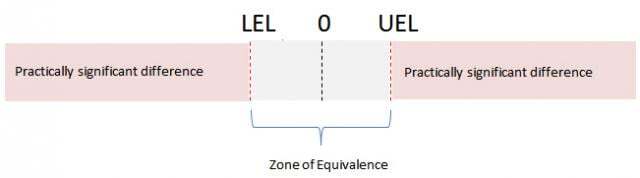
Der Äquivalenzbereich wird durch eine untere und/oder obere Äquivalenzgrenze definiert. Die untere Äquivalenzgrenze (UÄG) legt die Untergrenze für eine akzeptable Differenz fest. Die obere Äquivalenzgrenze (OÄG) legt die Obergrenze für eine akzeptable Differenz fest. Jede Differenz vom Mittelwert, die in diesen Bereich fällt, wird als unwichtig betrachtet.

In einigen Branchen, z. B. der Pharmaindustrie, werden die Äquivalenzgrenzen behördlich vorgegeben. Wenn für Ihre Anwendung keine Richtlinien vorliegen, müssen Sie auf Kenntnisse Ihres Produkts oder Prozesses zurückgreifen, um den Äquivalenzbereich festzulegen.

Leider gilt dabei: Es gibt auf der ganzen Welt keinen Statistiker, der Ihnen dabei helfen kann, diese Grenzen festzulegen. Denn dies ist keine statistische Fragestellung. Vielmehr geht es darum, wie groß eine Differenz sein muss, damit greifbare Konsequenzen für Sie oder Ihre Kunden entstehen.

Eine Differenz von 0,005 mg vom Soll-Mittelwert? Eine Verschiebung des Prozessmittelwerts um 10 %? Es sollte offensichtlich sein, dass für den Durchmesser von Stents z. B. andere Kriterien als für den Durchmesser von Getränkedosen herangezogen werden.

ÄQUIVALENZTESTS IN DER PRAXIS

Hier ist ein kurzes Beispiel für einen Äquivalenztest bei einer Stichprobe, das in abgewandelter Form aus der Minitab-Hilfe übernommen wurde. Um das Beispiel nachzuvollziehen, können Sie die überarbeiteten Datenhier herunterladen. Wenn Sie nicht über Minitab Statistical Software verfügen, können Sie hier eine kostenlose Demoversion herunterladen.

Angenommen, ein Verpackungsunternehmen möchte sicherstellen, dass die zum Öffnen ihrer Snackbeutel benötigte Kraft innerhalb von 10 % des Sollwerts von 4,2 N (Newton) liegt. Aus früheren Tests ist bekannt, dass sich die Beutel bei einer Kraft von mehr als 10 % unter dem Sollwert zu einfach öffnen und dies die Frische des Produkts beeinträchtigt. Eine Kraft von mehr als 10 % über dem Sollwert bedeutet, dass sich die Beutel zu schwer öffnen lassen. Bei einer Zufallsstichprobe von 100 Beuteln wird die Kraft gemessen, die jeweils zum Öffnen erforderlich ist.

Um zu testen, ob die mittlere Kraft dem Sollwert entspricht, wählen die Analytiker „Statistik“ > „Äquivalenztests“ > „1 Stichprobe“ aus und füllen das Dialogfeld wie unten gezeigt aus:

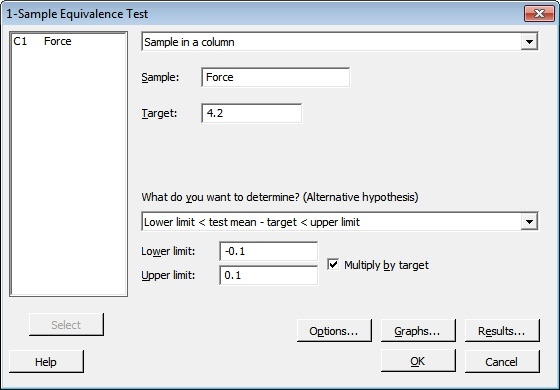
Tipp: Verwenden Sie das Feld Mit Sollwert multiplizieren, wenn Sie die Äquivalenzgrenzen für die Differenz als Prozentsatz des Sollwerts festlegen möchten. Im vorliegenden Fall ist die Untergrenze 10 % kleiner als der Sollwert. Die Obergrenze ist 10 % größer als der Sollwert. Wenn Sie die Äquivalenzgrenzen mit Zahlenwerten, nicht mit Prozentsätzen festlegen möchten, geben Sie einfach die tatsächlichen Werte für die Äquivalenzgrenzen ein, und lassen Sie das Feld Mit Sollwert multiplizieren deaktiviert.

Nachdem Sie auf OK klicken, zeigt Minitab folgende Ergebnisse an:

Äquivalenztest, 1 Stichprobe: Kraft

Differenz: Mittelwert(Kraft ) - Sollwert

Differenz        SE     95% KI     Äquivalenzintervall
   0,14270  0,067559  (0; 0,25487)      (-0,42; 0,42)

KI liegt innerhalb des Äquivalenzintervalls. Äquivalenz kann angenommen werden.

Test
Nullhypothese:         Differenz ≤ -0,42 oder Differenz ≥ 0,42
Alternativhypothese:  -0,42 < Differenz < 0,42
α-Niveau:                 0,05

Nullhypothese     DF  t-Wert  p-Wert
Differenz ≤ -0,42  99   8,3290    0,000
Differenz ≥ 0,42   99  -4,1046    0,000

Der größere der beiden p-Werte ist 0,000. Äquivalenz kann angenommen werden.

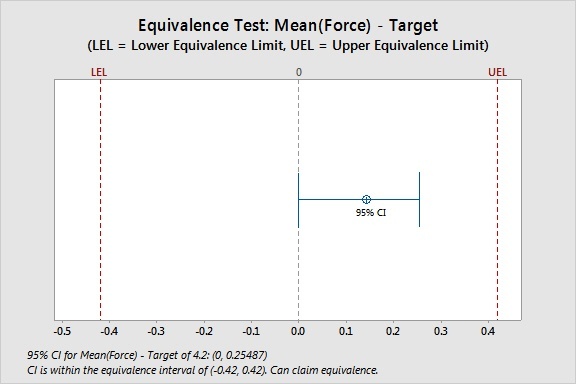
Da das Konfidenzintervall für die Differenz vollständig innerhalb der Äquivalenzgrenzen liegt, können Sie die Nullhypothese, dass der Mittelwert vom Sollwert abweicht, zurückweisen. Sie können behaupten, dass der Mittelwert und der Sollwert gleich sind.

Beachten Sie Folgendes: Hätten Sie diese Daten mit einem regulären t-Test bei einer Stichprobe analysiert, würde die Ausgabe eine statistisch signifikante Differenz zwischen dem Mittelwert und dem Sollwert zeigen (auf dem Signifikanzniveau 0,05):

t-Test bei einer Stichprobe: Kraft

Test bei μ = 4,2 vs ≠ 4,2
Variable    N    Mittelwert   StdAbw  SE des Mittelwerts       95% KI          t      p
Kraft         100  4,3427  0,6756   0,0676  (4,2086; 4,4768)  2,11  0,037

Diese unterschiedlichen Ergebnisse widersprechen sich allerdings nicht.

Bei dem Äquivalenztest wurde die „Äquivalenz“ zwischen dem Mittelwert und dem Sollwert etwas weiter ausgelegt; dabei wurden die Werte verwendet, die Sie für den Äquivalenzbereich eingegeben haben. Beim regulären t-Test kommt keinerlei Wissen zum Tragen, was „praktisch signifikant“ bedeutet. Er kann die Differenz zum Sollwert daher nur in Bezug auf die statistische Signifikanz auswerten.

In dieser Hinsicht ist ein Äquivalenztest „intelligenter“ als ein regulärer t-Test. Durch Ihre Kenntnisse des Prozesses oder Produkts kann ein Äquivalenztest neben der statistischen Signifikanz auch noch die praktische Signifikanz einer Differenz auswerten.

WEITERE INFORMATIONEN ZU ÄQUIVALENZTESTS

Seit Kurzen sind in Minitab Statistical Software vier Arten von Äquivalenztests verfügbar. Wenn Sie mehr zu jedem dieser Tests erfahren möchten, wählen Sie Hilfe > Hilfe aus.

Klicken Sie auf die Registerkarte Index, führen Sie einen Bildlauf zu Äquivalenztests durch, und klicken Sie auf Übersicht.

Hinweis: Wenn Sie die Ausgabe oben betrachten, sehen Sie noch einen weiteren Punkt, in dem der Äquivalenztest von einem regulären t-Test abweicht. Die Nullhypothese wird mit zwei einseitigen t-Tests geprüft. Außerdem wird bei dem Test ein Äquivalenzbereich verwendet, der definiert, wie groß die Differenz zwischen Mittelwerten ist, die Sie als praktisch insignifikant betrachten. Dies werden wir im nächsten Beitrag genauer betrachte.

KURZE ZUSAMMENFASSUNG

Wenn Sie die Wahl zwischen einem Äquivalenztest und einem regulären t-Test haben, fragen Sie sich, was Sie belegen oder nachweisen möchten. Das, was wahr sein soll, muss als Alternativhypothese für den Test festgelegt werden, und dort muss die Beweislast liegen. Das Ergebnis, bei dem es weniger nachteilig ist, wenn es fälschlicherweise angenommen wird, muss die Nullhypothese sein. Wenn Sie klar beweisen möchten, dass zwei Mittelwerte gleich sind oder dass ein Mittelwert identisch mit einem Sollwert ist, sollten Sie eher einen Äquivalenztest als einen regulären t-Test wählen.

Möchten Sie Äquivalenztest in der aktuellen Version von Minitab ausprobieren?

Gute Herstellungspraxis in der Pharmazie:
regelkonforme kontinuierliche Prozessüberprüfung mit Minitab Solutions Analytics™

Hersteller von pharmazeutischen Produkten müssen ihre Prozesse kontinuierlich überprüfen (CPV), damit sie den regulatorischen Anforderungen (GMP) entsprechen und die Kundenvorgaben erfüllen. Nehmen Sie an unserem 60 minütigem Webinar am 15. September teil, um ein Beispiel für die Prozessverbesserung zur Erfüllung der Leistungsanforderungen aus der Praxis zu sehen. Melden Sie sich an >