Exponentialverteilung: Ausfalldaten mit schlechtem Gedächtnis

Mein Erinnerungsvermögen ist heute auch nicht mehr, was es mal war. Dazu kommt: Mein Erinnerungsvermögen ist heute auch nicht mehr, was es mal war.

Doch mein unheilbarer Fall von IHV („Ich hab's vergessen“) ist nicht so schlimm wie der der Exponentialverteilung.

Beim Modellieren von Ausfalldaten für die Zuverlässigkeitsanalyse hat die Exponentialverteilung überhaupt keine Erinnerung. Es wird nicht berücksichtigt, ob bereits vorher eine Einheit ausgefallen ist.

Das klingt erst einmal schlecht. Doch diese besondere Eigenschaft macht die Verteilung besonders geeignet zum Modellieren des Verhaltens von Einheiten mit einer konstanten Ausfallrate.

FEHLERDATEN MIT HILFE DER EXPONENTIALVERTEILUNG MODELLIEREN

Angenommen, Sie verfolgen die Zeit bis zum Ausfall für eine Stichprobe von Einheiten. Wenn Sie die Ergebnisse in einem Histogramm darstellen, sieht das ungefähr so aus:

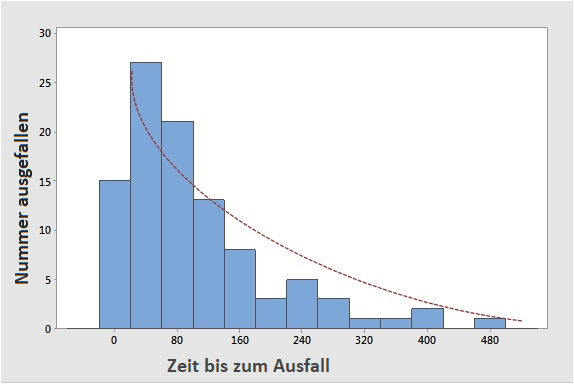
Sie sehen, dass die Anzahl von Einheiten, die zu einem bestimmten Zeitpunkt ausgefallen sind, im Lauf der Zeit abnimmt. Eine exponentielle Kurve kann sehr gut an diese kontinuierliche Abnahme angepasst werden.

Da die Abnahme gleichmäßig ist, würde sich bei einer Darstellung des sofortigen Ausfallrisikos einer beliebigen Einheit zu einem beliebigen Zeitpunkt (t) (als Hazard-Funktion bezeichnet) ein konstantes Ausfallrisiko zu jedem Zeitpunkt ergeben:

Der Ausfall einer Einheit zu einem vorherigen Zeitpunkt hat keine Auswirkungen auf das Ausfallrisiko zu einem anderen Zeitpunkt. Das bedeutet, dass die Exponentialverteilung gewissermaßen das Glück hat, sich nicht an vorherige Ausfälle zu „erinnern“. (Jeder Tag ist völlig neu, wenn Sie exponentiell verteilt sind! Keine Vorbelastungen!)

Aus diesem Grund stellt die Exponentialverteilung in der Zuverlässigkeitsanalyse häufig ein gutes Modell für ein Produkt oder ein Teil dar, das jederzeit ausfallen kann – unabhängig davon, ob es völlig neu, ein Jahr oder mehrere Jahre alt ist. Bei einer solchen Einheit wird nicht erwartet, dass sie während der vorgesehenen Anwendung altert oder verschleißt. Ein Beispiel wäre eine Komponente in einem Produkt, die normalerweise erst deutlich nach dem Produkt verschleißt.

Wenn allerdings erwartet wird, dass eine Komponente während der erwarteten Lebensdauer des Produkts altert, korrodiert oder verschleißt, ist die Exponentialverteilung kein geeignetes Modell, da das Ausfallrisiko mit der Zeit zunimmt.

Fallstudie in englischer Sprache: Time-to-Market and Design for Reliability at the Speed of Light in Signify (Markteinführungszeit und Design for Reliability in Lichtgeschwindigkeit bei Signify).
Sehen Sie sich die Aufzeichnung des Webinars in englischer Sprache an >

EINE VERTEILUNG AUSWÄHLEN: PRAKTISCHES KNOW-HOW + WAHRSCHEINLICHKEITSNETZE

Die Exponentialverteilung ist nur eine von mehreren Verteilungen, die häufig zum Modellieren von Ausfalldaten in der Zuverlässigkeitsanalyse eingesetzt werden. Eine Verteilung auszuwählen, mit der Ihre Daten gut modelliert werden, ist unabdingbare Voraussetzung für die Analyse.

Mit der Verteilungsidentifikation in Minitab können Sie die Anpassung verschiedener Verteilungen auswerten: Statistik > Zuverlässigkeit/Lebensdauer > Verteilungsanalyse. Wenn die Punkte in einer geraden Linie entlang der angepassten Verteilungslinie liegen, kann die Verteilung gut geeignet sein.

Die Grafiken unten zeigen, dass die Exponentialverteilung für die Ausfalldaten deutlich besser geeignet ist als die Normalverteilung.

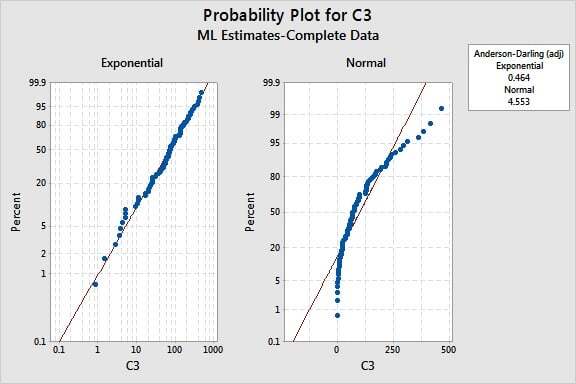
Beim Arbeiten mit Wahrscheinlichkeitsnetzen ist es möglich, dass mehrere Verteilungen gut für Ihre Daten geeignet sind. Um Ihre Entscheidung zu fällen, ist es daher sinnvoll, wenn Sie mit den Hauptmerkmalen und wichtigsten Anwendungsgebieten der Verteilungen vertraut sind.

ERINNERN SIE SICH NOCH DARAN, WAS SIE GERADE GELESEN HABEN?

Glücklicherweise müssen Sie sich nicht alle Eigenschaften jeder Verteilung merken. Sparen Sie sich den wertvollen Speicherplatz in Ihrem Gehirn stattdessen auf, um an den Muttertag zu denken, und setzen Sie einfach ein Lesezeichen für diese ausführliche Erläuterung im Minitab-Support: Exponentialverteilung in der Zuverlässigkeitsanalyses.

Steht Ihre Organisation vor Herausforderungen bei der Zuverlässigkeit? Laden Sie unser White Paper herunter, um die 5 Methoden kennenzulernen, durch die Sie mit Hilfe der Minitab Solutions Analytics eine zuverlässige Produktdesign entwickeln.