Mit einer Varianzanalyse (ANOVA) kann bestimmt werden, ob die Mittelwerte von drei oder mehr Gruppen unterschiedlich sind. Mit einer ANOVA wird die Gleichheit von Mittelwerten anhand von F-Tests statistisch überprüft. In diesem Beitrag wird die Funktionsweise von ANOVA und F-Tests am Beispiel einer einfachen ANOVA gezeigt.
Aber warten Sie ... Haben Sie sich jemals gefragt, warum mit einer Analyse der Varianz ermittelt werden soll, ob die Mittelwerte unterschiedlich sind? Neben der Antwort auf diese Frage geht es in diesem Beitrag darum, welche Informationen Varianzen über Mittelwerte bereitstellen.
Wie in meinen Beiträgen zu den Grundlagen von t-Tests soll der Schwerpunkt bei der ANOVA und den F-Tests auf Konzepten und Grafiken und nicht auf Gleichungen liegen.
Was sind F-Statistiken und der F-Test?
F-Tests sind nach der F-Statistik benannt, die wiederum nach Sir Ronald Fisher benannt wurde. Die F-Statistik zeigt einfach das Verhältnis von zwei Varianzen. Varianzen sind ein Maß für die Streuung, d. h. wie weit vom Mittelwert entfernt Daten verteilt sind. Größere Werte stehen für eine stärkere Streuung.
Die Varianz ist die quadrierte Standardabweichung. Standardabweichungen sind für uns leichter zu verstehen als Varianzen, weil sie in den gleichen Einheiten wie die Daten und nicht in quadrierten Einheiten dargestellt werden. Bei vielen Analysen werden allerdings Varianzen in den Berechnungen verwendet.
F-Statistiken beruhen auf dem Verhältnis der Mittel der Quadrate. Der Begriff „Mittel der Quadrate“ kann verwirrend klingen. Es handelt sich aber einfach um einen Schätzwert für die Varianz der Grundgesamtheit, bei dem die Freiheitsgrade (DF), mit denen dieser Schätzwert berechnet wurde, berücksichtigt werden.
Auch wenn es sich um ein Verhältnis von Varianzen handelt, können Sie F-Tests in einer Vielzahl von Situationen anwenden. Wenig überraschend kann mit einem F-Test die Gleichheit von Varianzen bewertet werden. Da jedoch andere Varianzen in dem Verhältnis genutzt werden, bietet ein F-Test äußerst flexible Analysemöglichkeiten. So können Sie z. B. mit F-Statistiken und F-Tests die Gesamtsignifikanz eines Regressionsmodells prüfen, die Anpassungen verschiedener Modelle vergleichen, bestimmte Regressionsterme testen und die Gleichheit von Mittelwerten prüfen.
Verwenden des F-Tests in einer einfachen ANOVA
Wenn Sie mit einem F-Test ermitteln möchten, ob die Gruppenmittelwerte gleich sind, müssen Sie nur die entsprechenden Varianzen in das Verhältnis aufnehmen. Bei einer einfachen ANOVA ist die F-Statistik das folgende Verhältnis:
F = Streuung zwischen Stichprobenmittelwerten/Streuung innerhalb der Stichproben
Dieses Verhältnis lässt sich am besten verstehen, indem wir ein Beispiel für eine einfache ANOVA durchgehen.
Wir analysieren dabei vier Kunststoffstichproben, um zu ermitteln, ob die mittlere Festigkeit unterschiedlich ist. Sie können die Beispieldaten herunterladen, wenn Sie die Analyse selbst durchführen möchten. (Wenn Sie nicht über Minitab verfügen, können Sie eine kostenlose 30-Tage-Demoversion herunterladen.) Beim Erläutern der Konzepte werde ich auf die Ausgabe dieser einfachen ANOVA zurückkommen.
Wählen Sie in Minitab Statistik > Varianzanalyse (ANOVA) > Einfache ANOVA... aus. Wählen Sie im Dialogfeld „Festigkeit“ als Antwort und „Stichprobe“ als Faktor aus. Klicken Sie auf „OK“. Im Sessionfenster von Minitab sehen Sie die folgende Ausgabe:
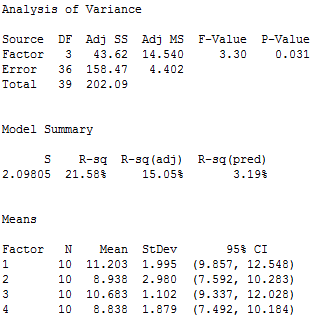
Zähler: Streuung zwischen Stichprobenmittelwerten
Mit der einfachen ANOVA wurde ein Mittelwert für jede der vier Kunststoffstichproben berechnet. Die Gruppenmittelwerte lauten wie folgt: 11,203; 8,938; 10,683 und 8,838. Diese Gruppenmittelwerte sind um den Gesamtmittelwert für alle 40 Beobachtungen verteilt, der bei 9,915 liegt. Liegen die Gruppenmittelwerte dicht am Gesamtmittelwert, ist ihre Streuung gering. Sind die Gruppenmittelwerte jedoch weiter weg vom Gesamtmittelwert verteilt, ist ihre Streuung höher.
Wenn wir zeigen möchten, dass die Gruppenmittelwerte unterschiedlich sind, ist es natürlich gut, wenn die Mittelwerte weiter voneinander entfernt sind. Anders ausgedrückt, ist eine höhere Streuung der Mittelwerte erwünscht.
Stellen Sie sich vor, dass wir zwei unterschiedliche einfache ANOVAs durchführen, bei denen jede Analyse vier Gruppen umfasst. Die Grafik unten zeigt die Verteilung der Mittelwerte. Jeder Punkt steht für den Mittelwert einer ganzen Gruppe. Je weiter die Punkte ausgebreitet sind, umso höher ist der Wert der Streuung im Zähler der F-Statistik.

Mit welchem Wert messen wir die Varianz zwischen den Stichprobenmittelwerten für das Beispiel mit der Kunststofffestigkeit? In der Ausgabe der einfachen ANOVA verwenden wir das korrigierte Mittel der Quadrate (Korr MS) für den Faktor, d. h. 14,540. Versuchen Sie nicht, diese Zahl zu interpretieren, da sie keinen Sinn ergeben wird. Sie entspricht der Summe der quadrierten Abweichungen geteilt durch die DF für den Faktor. Merken Sie sich einfach, dass dieser Wert immer größer wird, je weiter auseinander die Gruppenmittelwerte liegen.
Nenner: Streuung innerhalb der Stichproben
Wir benötigen auch einen Schätzwert für die Streuung innerhalb der einzelnen Stichproben. Zum Berechnen dieser Streuung müssen wir ermitteln, wie weit jede Beobachtung vom Gruppenmittelwert für alle 40 Beobachtungen entfernt ist. Technisch ist dies die Summe der quadrierten Abweichungen für jede Beobachtung vom Gruppenmittelwert geteilt durch die DF für den Fehler.
Liegen die Beobachtungen für jede Gruppe nahe am Gruppenmittelwert, ist die Streuung innerhalb der Stichproben gering. Liegen die Beobachtungen für jede Gruppe jedoch weiter weg vom Gruppenmittelwert, ist die Streuung innerhalb der Stichproben größer.
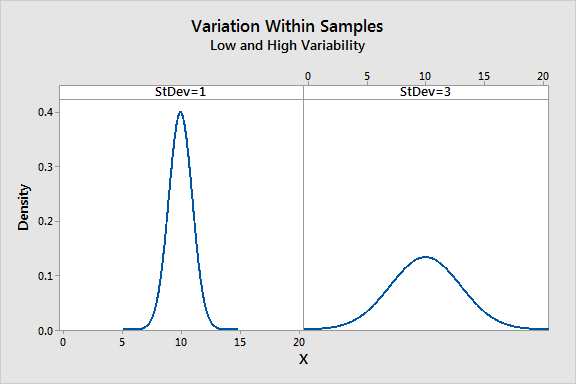
In der Grafik zeigt der linke Bereich eine geringe Streuung und der rechte Bereich eine starke Streuung in den Stichproben. Je weiter die Beobachtungen vom jeweiligen Gruppenmittelwert entfernt sind, umso höher ist der Wert im Nenner der F-Statistik.
Wenn wir zeigen möchten, dass die Mittelwerte unterschiedlich sind, sollte die Streuung innerhalb der Gruppen also möglichst gering sein. Sie können sich die Varianz innerhalb einer Gruppe als Hintergrundgeräusch vorstellen, das eine Differenz zwischen Mittelwerten verdecken kann.
In diesem Beispiel einer einfachen ANOVA verwenden wir als Wert für die Varianz innerhalb der Stichproben das korrigierte Mittel der Quadrate (Korr MS) für den Fehler, in diesem Fall 4,402. Dies wird als „Fehler“ betrachtet, weil es sich um die Streuung handelt, die nicht vom Faktor erklärt wird.
F-Statistik: Streuung zwischen Stichprobenmittelwerten/Streuung innerhalb der Stichproben
Die F-Statistik ist die Teststatistik für F-Tests. Allgemein ist eine F-Statistik das Verhältnis von zwei Größen, von denen unter der Nullhypothese erwartet wird, dass sie ungefähr gleich sind. Hiermit wird eine F-Statistik von ungefähr 1 erzeugt.
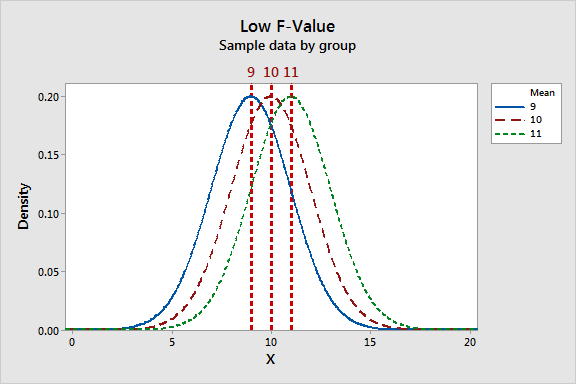
Die F-Statistik umfasst beide Maße für die Streuung, die oben beschrieben wurden. Betrachten wir nun, wie diese Größen zusammenspielen, um niedrige und hohe F-Werte zu erzeugen. Vergleichen Sie in den Grafiken unten die Spannweite der Gruppenmittelwerte mit der Spannweite innerhalb jeder Gruppe.
 |
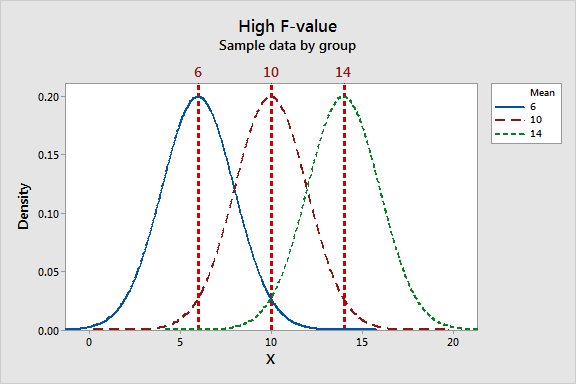 |
Die Grafik mit dem niedrigen F-Wert zeigt einen Fall, in dem die Gruppenmittelwerte im Verhältnis zur Streuung innerhalb der einzelnen Gruppen näher zusammen liegen (geringe Streuung). Die Grafik mit dem hohen F-Wert zeigt einen Fall, in dem die Streuung der Gruppenmittelwerte relativ zur Streuung innerhalb der Gruppen groß ist. Um die Nullhypothese, dass die Gruppenmittelwerte gleich sind, abzulehnen, wird ein hoher F-Wert benötigt.
Im Beispiel mit der Kunststofffestigkeit verwenden wir das korrigierte Mittel der Quadrate (Korr MS) für den Faktor als Zähler (14,540) und das korrigierte Mittel der Quadrate (Korr MS) für den Fehler als Nenner (4,402). Dies führt zu einem F-Wert von 3,30.
Ist der F-Wert ausreichend hoch? Es ist schwierig, einen einzelnen F-Wert zu interpretieren. Der F-Wert muss in einem größeren Kontext betrachtet werden, um ihn interpretieren zu können. Hierfür berechnen wir unter Verwendung der F-Verteilung Wahrscheinlichkeiten.
F-Verteilungen und Hypothesentests
Bei der einfachen ANOVA folgt das Verhältnis zwischen der Streuung zwischen verschiedenen Gruppen und der Streuung innerhalb der Gruppen einer F-Verteilung, wenn die Nullhypothese wahr ist.
Wenn Sie eine einfache ANOVA für eine einzelne Studie durchführen, erhalten Sie nur einen F-Wert. Wenn wir allerdings mehrere gleich große Zufallsstichproben aus der gleichen Grundgesamtheit nehmen und die gleiche einfache ANOVA durchführen, erhalten wir mehrere F-Werte und können die Verteilung dieser Werte grafisch darstellen. Eine solche Verteilung wird als Stichprobenverteilung bezeichnet.
Da bei der F-Verteilung angenommen wird, dass die Nullhypothese wahr ist, können wir den F-Wert aus der Studie in der F-Verteilung verwenden, um zu bestimmen, inwiefern die Ergebnisse der Nullhypothese entsprechen, und um Wahrscheinlichkeiten zu berechnen.
Die Wahrscheinlichkeit, die dabei berechnet werden soll, ist die Wahrscheinlichkeit, eine F-Statistik zu erhalten, die mindestens so hoch wie der Wert ist, der bei der Studie ermittelt wurde. Anhand dieser Wahrscheinlichkeit können wir ermitteln, wie häufig oder selten der F-Wert unter der Annahme einer wahren Nullhypothese ist. Wenn die Wahrscheinlichkeit ausreichend niedrig ist, können wir schließen, dass die Daten nicht der Nullhypothese entsprechen. Die Anzeichen in den Stichprobendaten sind ausreichend stark, um die Nullhypothese für die gesamte Grundgesamtheit zurückzuweisen.
Die Wahrscheinlichkeit, die wir hier berechnen, wird auch als p-Wert bezeichnet!
Zum Darstellen der F-Verteilung für das Beispiel mit der Kunststofffestigkeit verwende ich die Darstellungen der Wahrscheinlichkeitsverteilung in Minitab. Um die F-Verteilung darzustellen, die für dieses Design und den Stichprobenumfang geeignet ist, müssen wir den richtigen DF-Wert angeben. In der Ausgabe der einfachen ANOVA können wir 3 DF für den Zähler und 36 DF für den Nenner erkennen.
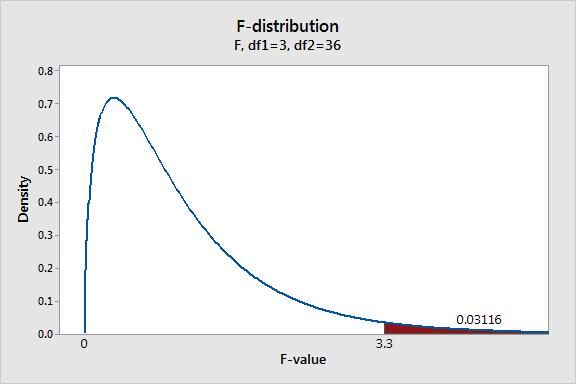
Die Grafik zeigt die Verteilung von F-Werten, die wir erhalten, wenn die Nullhypothese wahr ist und die Studie viele Male wiederholt wird. Der eingefärbte Bereich zeigt die Wahrscheinlichkeit, einen F-Wert zu erhalten, der mindestens so groß wie der Wert ist, der bei der Studie ermittelt wurde. Wenn die Nullhypothese wahr ist, liegen die F-Werte in ungefähr 3,1 % der Fälle in diesem eingefärbten Bereich. Diese Wahrscheinlichkeit ist ausreichend gering, um die Nullhypothese mit einem typischen Signifikanzniveau von 0,05 zurückzuweisen. Wir können schließen, dass nicht alle Gruppenmittelwerte gleich sind.
Informationen zum richtigen Interpretieren des p-Werts >>
Bewerten von Mittelwerten durch die Analyse der Streuung
Bei der ANOVA wird mit einem F-Test bestimmt, ob die Streuung zwischen Gruppenmittelwerten größer als die Streuung der Beobachtungen innerhalb der Gruppen ist. Wenn dieses Verhältnis hinreichend groß ist, können Sie schließen, dass nicht alle Mittelwerte gleich sind.
Dies führt uns zurück zur Frage, warum wir die Streuung analysieren, um Aussagen über Mittelwerte zu treffen. Betrachten Sie die folgende Frage: „Sind die Gruppenmittelwerte unterschiedlich?“ Damit stellen Sie implizit eine Frage zur Streuung der Mittelwerte. Denn wenn sich die Gruppenmittelwerte nicht – oder nicht mehr als aufgrund von Zufallseffekten erwartbar – unterscheiden, können Sie nicht sagen, dass die Mittelwerte unterschiedlich sind. Und deshalb analysieren Sie die Varianz, um die Mittelwerte zu prüfen.





