Dies ist der zweite Teil einer Reihe. Teil 1 finden Sie hier.
Im ersten Teil habe ich mit der Minitab Statistical Software ein Regressionsmodell entwickelt, das die Beziehung zwischen dem Body Mass Index (BMI) und dem Körperfettanteil beschreibt. In diesem Beitrag prognostiziere ich anhand dieses Modells den Körperfettanteil und beurteile die Genauigkeit meiner Prognosen. Außerdem werde ich die Prognosen von Minitab mit denen von Waagen vergleichen, die den Körperfettanteil mit Hilfe einer bioelektrischen Impedanzanalyse (BIA) schätzen.
PROGNOSTIZIERTES R-QUADRAT BEURTEILEN
Zuvor habe ich eine Darstellung der Anpassungslinie verwendet, um das Modell auszuwerten. Die Prognosen werde ich mit demselben Modell erstellen, doch ich muss eine allgemeine Regression verwenden. Mit der allgemeinen Regression erhalten wir eine weitere Ausgabe, die ausschlaggebend für Prognosen ist: das prognostizierte R-Quadrat. Dieser Wert gibt an, wie gut das Modell neue Beobachtungen prognostiziert. Hier sehen Sie die Modellübersicht aus der allgemeinen Regression.
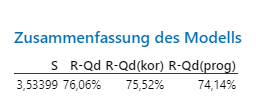
Für das Modell beträgt das prognostizierte R-Quadrat 74,14 %. Da dieser Wert nah am zuvor ermittelten R-Quadrat von 76,06 % liegt, liefert das Modell also gültige Prognosen.
Wenn bei einem Modell das normale R-Quadrat gut, das prognostizierte R-Quadrat jedoch deutlich geringer ist, deutet dies darauf hin, dass das Modell an die ursprünglichen Daten angepasst ist, aber keine gültigen Prognosen liefert. Dies passiert häufig, wenn das Modell zu kompliziert ist und das Rauschen in den Daten abbildet. Dies wird als „übermäßige Anpassung“ bezeichnet. Prüfen Sie daher das prognostizierte R-Quadrat, bevor Sie Prognosen erstellen!
EINSCHRÄNKUNGEN BEI DER PROGNOSE MIT DER REGRESSION
Bevor wir beginnen, sollten wir noch einige wichtige Punkte betrachten. Zunächst einmal gelten Regressionsprognosen nur für die Spannweite, die von den Originaldaten abgedeckt wird. Wir sollten daher nur Prognosen für BMI-Werte zwischen 15 und 35 treffen. Prognosen gelten außerdem nur für die Grundgesamtheit, die in den Daten abgebildet wird. In diesem Fall sind dies Mädchen im Alter zwischen 12 und 14 Jahren.
Wir kennen die Beziehung zwischen BMI und Körperfettanteil nur in diesem Datenbereich und für diese Grundgesamtheit. Jenseits davon könnte sich die Kurve ändern, was die Prognosen ungenau machen würde. Anders ausgedrückt wissen wir nicht mehr als das, was wir tatsächlich messen.
PROGNOSEN MIT DER ALLGEMEINEN REGRESSION
Wir haben ein gutes Modell mit einem guten prognostizierten R-Quadrat. Wir können also eine Prognose erstellen! In der Minitab Statistiksoftware wähle ich Statistik > Regression > Allgemeine Regression aus. Dann fülle ich das Dialogfeld Prognose wie folgt aus, um den prozentualen Körperfettanteil bei einem BMI von 18 zu prognostizieren
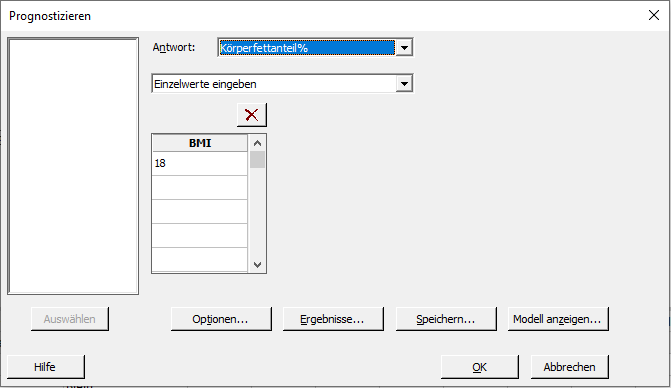
Wir erhalten die folgende Ausgabe:

Bei einem BMI von 18 liegt der prognostizierte (oder angepasste) Körperfettanteil bei ca. 23 %. Doch wie genau ist diese Prognose? Minitab bietet hierzu zwei Werte:
Das Prognoseintervall (PI)strong> stellt den Bereich dar, in dem eine einzelne neue Beobachtung wahrscheinlich liegen wird. Wir können also zu 95 % sicher sein, dass der Körperfettanteil einer bestimmten Person zwischen 16 % und 30 % (oder +/- 7 %) liegt, wenn ihr BMI 18 beträgt.
Das Konfidenzintervall (KI)strong> stellt den Bereich dar, in dem der Mittelwert wahrscheinlich liegen wird. Wir können zu 95 % sicher sein, dass der mittlere Körperfettanteil aller Mädchen in dieser Altersgruppe, die einen BMI von 18 haben, zwischen 22,1 % und 23,9 % (oder ungefähr +/- 1 %) liegt
Das Prognoseintervall ist immer breiter als das entsprechende Konfidenzintervall. Dies ist auf die zusätzliche Ungewissheit beim Prognostizieren eines einzelnen Werts gegenüber dem Mittelwert zurückzuführen.
VERGLEICH DER MINITAB-PROGNOSEN MIT DEN SCHÄTZUNGEN VON BIA-WAAGEN
Der vom DXA-Gerät gemessene Körperfettanteil ist der tatsächliche und genaue Messwert. Sowohl die BMI-Regressionsanalyse als auch die BIA-Waagen versuchen, den Körperfettanteil zu schätzen. Vergleichen wir daher jetzt die Genauigkeit und Präzision der Prognosen aus der Regression mit der der BIA-Waagen.
Wenn Sie eine solche Waage nutzen, geben Sie Geschlecht und Größe ein, und die Waage misst Ihr Gewicht. Außerdem fließt ein geringer Strom durch Ihren Körper, um den Fettanteil zu schätzen. Ich habe die Probandinnen nicht mit einer solchen Waage messen können, da dies bei diesem Projekt nicht vorgesehen war. Ich habe allerdings auf verschiedenen Websites (hier und hier) recherchiert, auf denen Experten im Bereich Energiestoffwechsel und Bewegung zu diesen Waagen befragt wurden. Es gibt verschiedene Möglichkeiten zum Vergleichen der beiden Methoden. Die fettgedruckten Aussagen beziehen sich auf Fehler in den Messungen der BIA-Waagen, danach folgt ein Vergleich mit den Minitab-Prognosen.
Die Waagen berechnen Schätzungen mit größeren Fehlern bei besonders schlanken und stark übergewichtigen Menschen.
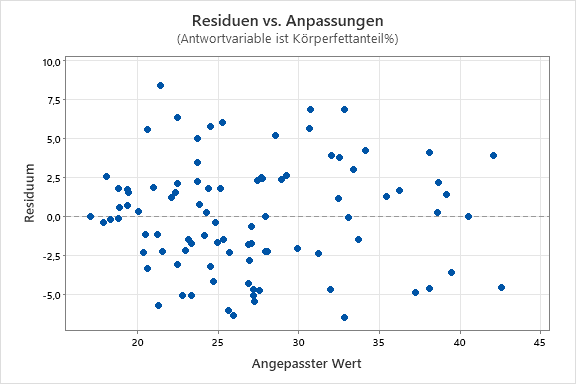
Dieses Problem wird als nicht konstante Varianz oder Heteroskedastizität bezeichnet. In den Minitab-Prognosen auf der Grundlage dieses Modells tritt dieses Problem nicht auf. Wir prüfen sogar immer auf diesen Umstand, wenn ein Regressionsmodell angepasst wird, indem wir auf die Residuendiagramme zurückgreifen. Zum Prüfen auf Heteroskedastizität betrachten wir das Diagramm der Residuen im Vergleich zu den Anpassungen (unten). Wir können sehen, ob die Residuen sich am oberen oder unteren Rand der Spannweite breiter verteilen. Im Diagramm unten sehen wir allerdings eine gleichmäßige Verteilung (oder Varianz) um Null, was auf die gewünschte Homoskedastizität hinweist.
Die Waagen tendieren dazu, den Körperfettanteil von sehr schlanken Personen zu überschätzen und den von Übergewichtigen zu unterschätzen.
Diese Art von systematischen Fehlern wird als systematische Messabweichung bezeichnet. In den Minitab-Prognosen auf der Grundlage dieses Modells tritt dieses Problem nicht auf. Dies ist ein weiterer Punkt, den wir beim Anpassen von Regressionsmodellen immer beurteilen. Hierzu betrachten wir das Diagramm der Residuen im Vergleich zu den Anpassungen (oben). Wenn die systematische Messabweichung in unserem Modell der der Waagen entspricht, müssten wir ein Muster in den Residuen erkennen können. Im Diagramm wären in diesem Fall mehr positive Residuen auf der linken Seite und mehr negative auf der rechten Seite zu sehen. Wir sehen hier aber Residuen, die über die gesamte Spannweite zufällig nach oben und unten verteilt sind, was darauf hinweist, dass keine systematische Messabweichung vorliegt.
Die Waagen liefern Schätzungen des tatsächlichen Körperfettanteils, die um +/- 5 % abweichen können.
Wir haben herausgefunden, dass die Prognosen unseres Regressionsmodells für eine Person um +/- 7 % abweichen können. Es gibt hier allerdings eine wichtige Einschränkung: Wir wissen, dass die Minitab-Prognosen mit einer Konfidenz von 95 % in diesem Intervall liegen, das Konfidenzniveau für die Schätzungen der Waagen konnte ich aber nicht ermitteln. Die Größe der Intervalle ist allerdings vergleichbar. Ich verkünde also einen Gleichstand.
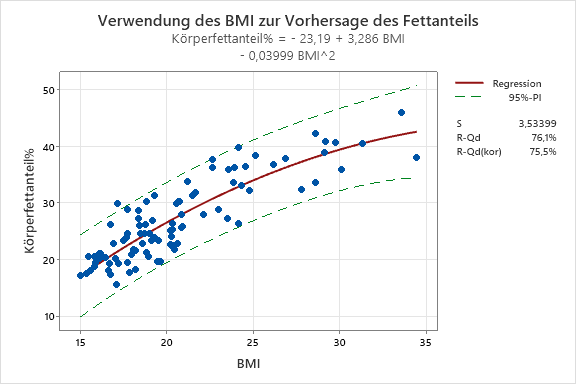
Ich habe das Prognoseintervall in der Darstellung der Anpassungslinie unten abgebildet, um zu zeigen, dass die Breite des Prognoseintervalls im gesamten Datenbereich fast konstant bleibt.
Die Waagen liefern Schätzungen, die sehr instabil sein können, wenn Sie sich nicht an strenge Vorgaben halten. Sie müssen die Waage bei immer gleicher Feuchtigkeit, zu einer bestimmten Uhrzeit und zu einem bestimmten Zeitpunkt des Menstruationszyklus nutzen. Außerdem dürfen Sie in den Stunden vor der Messung keinen Sport machen oder duschen.
Die Minitab-Prognosen weisen dieses Stabilitätsproblem nicht auf, weil sie ganz klar nicht von diesen Faktoren abhängen. Bei diesem Modell wird ein BMI von 18 immer dieselbe Schätzung liefern. Darüber hinaus sollten die Schätzungen gültig sein, weil das prognostizierte R-Quadrat fast identisch mit dem R-Quadrat ist.
SCHLUSSBEMERKUNGEN ZU PROGNOSEN MIT DER REGRESSION
Bei beiden Verfahren werden Größe, Gewicht, Geschlecht und Alter berücksichtigt (unser Modell bezieht sich auf Mädchen im Teenageralter). Bei BIA-Waagen kommt das elektrische Signal dazu, doch aus meiner Sicht führt dies nur zu mehr Rauschen bei den Ergebnissen. Im besten Fall, d. h., wenn die Anwendungsvorgaben für BIA-Waagen genau eingehalten werden und die betrachtete Person nicht ungewöhnlich schlank oder übergewichtig ist, können die BMI-Werte und die Waagen Prognosen mit ähnlich großen Prognoseintervallen liefern. Bei extremeren Werten oder wenn die Vorgaben nicht eingehalten werden, führen die elektrischen Signale zu stark schwankenden Ergebnissen, und die Minitab-Prognosen gewinnen einen Vorteil.
Bevor wir allerdings unser Modell als Ersatz für die Waagen anbieten, müssen wir daran denken, dass das Modell nur für Mädchen in einem bestimmten Alter gilt. Um es auf männliche Probanden und andere Altersgruppen anwenden zu können, ist noch viel Arbeit nötig. Wir haben sozusagen eine Pilotstudie durchgeführt, die die Machbarkeit des Ansatzes belegt.
Wenn Sie etwas über Regression lernen wollen, schauen Sie sich unsere Schulungskurse zu diesem Thema an! Weiterlesen




