Nachdem Sie ein lineares Modell mit einer Regressionsanalyse, ANOVA oder Versuchsplanung (DOE) angepasst haben, müssen Sie ermitteln, wie gut das Modell an Ihre Daten angepasst ist. Hierfür stellt die Minitab Statistical Software verschiedene Statistiken zur Güte der Anpassung bereit. In diesem Beitrag gehen wir auf das R-Quadrat (R2 ) und einige seiner Einschränkungen ein – nicht ohne dabei ein paar Überraschungen zu entdecken. Ein niedriges R-Quadrat ist z. B. nicht immer schlecht und ein hohes R-Quadrat nicht immer gut!
Was ist die Güte der Anpassung für ein lineares Modell?
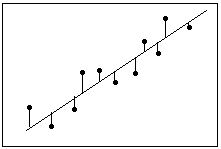Definition: Residuum = beobachteter Wert – angepasster WertBei der linearen Regression wird eine Gleichung berechnet, bei der der Abstand zwischen der Anpassungslinie und allen Datenpunkten minimiert wird. Technisch gesehen wird bei der Regression nach der Methode der kleinsten Quadrate (OLS) die Summe der quadrierten Residuen minimiert.
Im Allgemeinen ist ein Modell gut an die Daten angepasst, wenn die Differenzen zwischen den beobachteten Werten und den durch das Modell prognostizierten Werten klein und nicht verzerrt sind.
Bevor Sie allerdings die statistischen Maße für die Güte der Anpassung betrachten, sollten Sie die Residuendiagramme überprüfen. Residuendiagramme können unerwünschte Muster in den Residuen, die auf verzerrte Ergebnisse hinweisen, effektiver als Zahlen aufzeigen. Wenn die Residuendiagramme in Ordnung sind, können Sie den numerischen Ergebnissen vertrauen und sich den Maßen für die Güte der Anpassung zuwenden.
Was ist das R-Quadrat?
Das R-Quadrat ist ein statistisches Maß dafür, wie dicht die Daten an der angepassten Regressionslinie liegen. Es wird auch als Determinationskoeffizient oder – bei der multiplen Regression – als multipler Determinationskoeffizient bezeichnet.
Die Definition des R-Quadrat ist relativ einfach: Es handelt sich um den Prozentsatz der Streuung in der Antwortvariablen, der durch ein lineares Modell erklärt wird. Oder:
R-Quadrat = erklärte Streuung/Gesamtstreuung
Das R-Quadrat nimmt immer Werte von 0 bis 100 % an.
- 0 % gibt an, dass das Modell die Streuung in der Antwortvariablen bezogen auf den Mittelwert überhaupt nicht erklärt.
- 100% gibt an, dass das Modell die Streuung in der Antwortvariablen bezogen auf den Mittelwert vollständig erklärt.
Im Allgemeinen gilt: Je höher das R-Quadrat, desto besser ist das Modell an die Daten angepasst. Für diese Richtlinie gelten allerdings wichtige Einschränkungen, auf die ich in diesem und im nächsten Beitrag eingehen werde.
Grafische Darstellung des R-Quadrats
Durch das Abbilden der angepassten Werte im Vergleich zu den beobachteten Werten werden verschiedene Werte des R-Quadrats für Regressionsmodelle grafisch veranschaulicht.
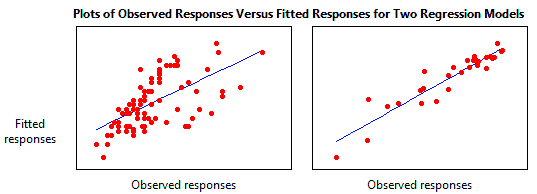
Das linke Regressionsmodell erklärt 38,0 % der Streuung, während das rechte Modell 87,4 % erklärt. Je größer der Prozentsatz, der durch das Regressionsmodell erklärt wird, desto näher liegen die Datenpunkte an der angepassten Regressionslinie. Wenn ein Modell theoretisch 100 % der Streuung erklären könnte, wären die angepassten Werte immer gleich den beobachteten Werten, und daher würden alle Datenpunkte auf der angepassten Regressionslinie liegen.
Wichtige Einschränkungen des R-Quadrats
Mit dem R-Quadrat kann nicht bestimmt werden, ob die Schätzwerte der Koeffizienten und die Prognosen verzerrt sind. Deshalb müssen Sie zusätzlich die Residuendiagramme betrachten.
Das R-Quadrat zeigt nicht, ob ein Regressionsmodell angemessen ist. Ein gutes Modell kann ein niedriges R-Quadrat aufweisen, und umgekehrt kann ein Modell, das nicht an die Daten angepasst ist, ein hohes R-Quadrat haben.
Das R-Quadrat in Ihrer Ausgabe ist ein verzerrter Schätzwert des R-Quadrats für die Grundgesamtheit.
Ist ein niedriges R-Quadrat grundsätzlich schlecht?
Nein! Es gibt zwei wichtige Gründe, warum ein niedriges R-Quadrat völlig unproblematisch sein kann.
In einigen Bereichen sind niedrige R-Quadrat-Werte sogar erwartbar. Beispielsweise liegen die R-Quadrat-Werte in allen Situationen, in denen menschliches Verhalten prognostiziert werden soll, z. B. in der Psychologie, normalerweise unter 50 %. Dies liegt daran, dass sich Menschen erheblich schlechter prognostizieren lassen als beispielsweise physikalische Prozesse.
Wenn das R-Quadrat niedrig ist, Sie aber über statistisch signifikante Prädiktoren verfügen, können Sie trotzdem wichtige Schlüsse dazu ziehen, wie Änderungen der Prädiktorwerte mit Änderungen der Werte der Antwortvariablen zusammenhängen. Unabhängig vom R-Quadrat stellen die signifikanten Koeffizienten die mittlere Änderung der Antwortvariablen dar, wenn die Prädiktorvariable eine Änderung in Höhe einer Einheit aufweist und die anderen Prädiktoren im Modell konstant bleiben. Auch diese Informationen bieten wertvolle Einblicke.
Hier finden Sie eine grafische Darstellung, die zeigt, warum ein niedriges R-Quadrat keine Auswirkungen auf die Interpretation der signifikanten Variablen hat.
Ein niedriges R-Quadrat ist am problematischsten, wenn Sie Prognosen erstellen möchten, die eine gewisse Präzision haben sollen (d. h. deren Prognoseintervall hin Wie hoch sollte das R-Quadrat für eine Prognose sein? Dies hängt von Ihren Anforderungen an die Breite des Prognoseintervalls sowie vom Ausmaß der Streuung in den Daten ab. Zwar wird für präzise Prognosen ein hohes R-Quadrat benötigt, doch wie wir sehen werden, ist dies nicht die einzige Voraussetzung.
Ist ein hohes R-Quadrat grundsätzlich gut?
Nein! Ein hohes R-Quadrat weist nicht unbedingt darauf hin, dass das Modell eine gute Anpassung aufweist. Dies mag überraschend sein, aber betrachten Sie einmal die Darstellung der Anpassungslinie und das Residuendiagramm unten. Die Darstellung der Anpassungslinie bildet die Beziehung zwischen der Elektronenbeweglichkeit in Halbleitern und dem natürlichen Logarithmus der Dichte in den experimentellen Daten eines Versuchs ab.
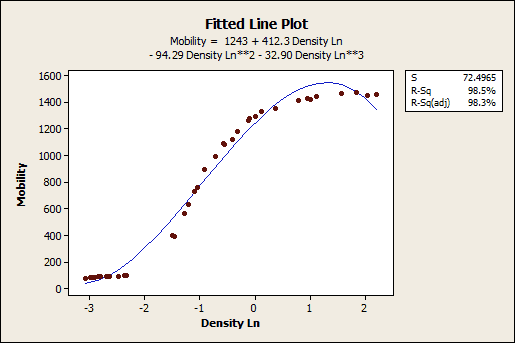
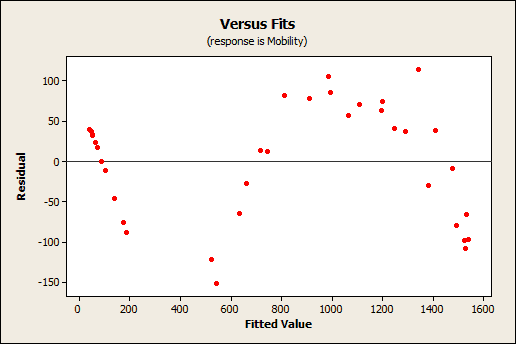
Die Darstellung der Anpassungslinie zeigt, dass die Daten eng einer Funktion folgen und dass das R-Quadrat 98,5 % beträgt – offenbar ein optimales Ergebnis. Betrachten Sie nun allerdings genauer, wie die Regressionslinie die Daten an unterschiedlichen Punkten entlang der Kurve systematisch zu hoch und zu niedrig prognostiziert (Verzerrung). Außerdem lassen sich im Diagramm der Residuen vs. Anpassungen Muster erkennen, wenn die Punkte eigentlich zufällig gestreut sein sollten. Dies weist auf eine schlechte Anpassung hin und ist eine wichtige Erinnerung daran, immer auch die Residuendiagramme zu überprüfen.
Dieses Beispiel stammt aus meinem Beitrag zur Entscheidung zwischen der linearen und nichtlinearen Regression. In diesem Fall sollte eine nichtlineare Regression verwendet werden, da lineare Modelle nicht an die spezifische Kurve angepasst werden können, der diese Daten folgen.
Ähnliche Verzerrungen können allerdings auch auftreten, wenn in einem linearen Modell wichtige Prädiktoren, Polynomialterme und Wechselwirkungsterme fehlen. Dies wird in der Statistik als Spezifikationsbias bezeichnet und durch ein unterspezifiziertes Modell verursacht. Für diese Art der Verzerrung können Sie die Residuen korrigieren, indem Sie dem Modell die entsprechenden Terme hinzufügen.
Weitere Informationen dazu, warum ein hohes R-Quadrat nicht immer gut ist, finden Sie in meinem Beitrag zu fünf Gründen, warum das R-Quadrat zu hoch sein kann.
Fazit zum R-Quadrat
Das R-Quadrat ist ein praktisches, scheinbar intuitiv verständliches Maß dafür, wie gut ein lineares Modell an eine Gruppe von Beobachtungen angepasst ist. Wie wir jedoch gesehen haben, ist das nicht die ganze Wahrheit. Sie sollten das R-Quadrat immer im Zusammenhang mit Residuendiagrammen, anderen Modellstatistiken und Fachwissen auswerten, um ein vollständiges Bild zu erhalten.
Das R-Quadrat ist eine Schätzung für die Stärke der Beziehung zwischen Ihrem Modell und der Antwortvariablen, kein formeller Hypothesentest für diese Beziehung. Mit dem F-Test für die Gesamtsignifikanz kann bestimmt werden, ob diese Beziehung statistisch signifikant ist.
Im nächsten Beitrag geht es weiter darum, dass das R-Quadrat allein nicht aussagekräftig ist, und wir betrachten zwei weitere Arten des R-Quadrats: das korrigierte R-Quadrat und prognostizierte R-Quadrat. Diese beiden Maße vermeiden bestimmte Probleme und stellen zusätzliche Informationen bereit, anhand derer Sie die Aussagekraft eines Regressionsmodells auswerten können.
