You may have been in a situation where you had created a general full factorial design and noticed that your design’s run size was higher than you imagined. (Quick refresher: a general full factorial design is an experimental design where any factor can have more than 2 levels).
Determined to minimize the monstrous size of your worksheet, you go back to Stat > DOE > Factorial > Create Factorial Design and go through all of the sub-menus to select a fractional factorial design. A fractional factorial design would allow you to select only a subset or "fraction" of the runs from your design to analyze.
You’d quickly find that there is no option to select a fractional subset for a general full factorial design. These fractional designs are only available in designs where each factor has 2 levels. We’ll need to start looking elsewhere for design reduction.
Fortunately, after creating a general full factorial design, a menu item ‘Select Optimal Design’ under DOE > Factorial > Create Factorial Design is now available in Minitab's statistical software. Select Optimal Design will allow you to select the "best" design points by reducing the number of experimental runs in the original design.
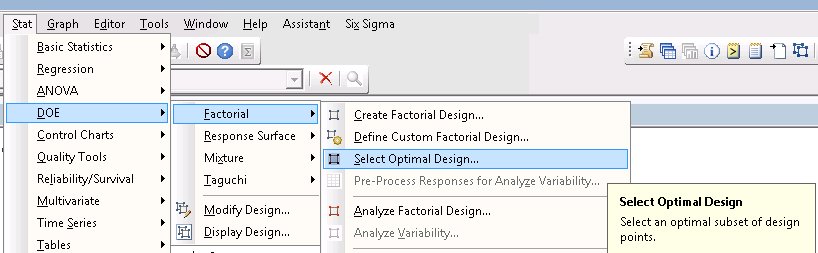
To obtain the best subset of your base set, you’ll need to focus on two things: points and terms.
Number of Points in Optimal Design
Enter in the number of runs you would like to subset out of your original design. For example, if your original design contains 64 runs, and you only have enough resources to capture 32 runs of data, enter 32.
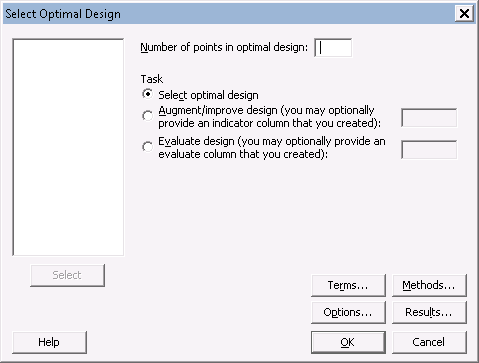
Terms
You’ll see a Terms… sub-menu. In here, you’ll see a model terms selection box. You’ll need to select an initial model prior to finding an optimal design. If you're looking to eventually analyze main effects and 2-way interactions, then you could select 2 from the 'Include terms in the model up through order' drop-down.
After clicking "OK" in each dialog window, Minitab will generate a new worksheet in your project, containing your optimal subset.
Optimality Measures
In your session window, you’ll see a table entitled Optimal Design:

The first section details the row numbers that were selected from your original general full factorial design. The second section is a listing of optimality measures, which are useful in comparing different designs to see which one is more appropriate. Let’s focus on D-optimality, as that it is the measure Minitab optimizes for.
D-optimality
D-optimality minimizes the variance in the regression coefficients of the fitted model. Larger values are desirable. The maximum possible value is n^(df), where n is the number of experimental runs and df is the degrees of freedom for all terms in your selected model plus the constant.
Where to go from here?
You may discover that after settling on a specific optimal design, you have room to collect 5 more runs from your original data set. You could select the task to ‘Augment/Improve’ within the Create Optimal Design menu to incorporate 5 new runs into your optimal design. This requires that you return back to your original design and create an indicator column to protect those points that were selected in the first optimal design. To protect these points, you need to use negative indicators such as “-1.” The rest of the points can be labeled as “0”, meaning that they can be excluded from the model when the design is reduced.
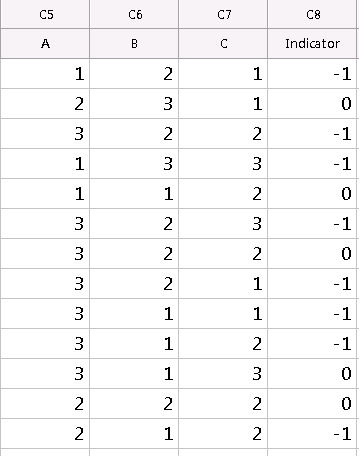
Selecting the task “Evaluate Design” under the Create Optimal Design menu can yield other benefits as well. This allows you to view how your D-optimality measures would change if you wanted to keep using the same optimal design points, but alter the model terms selected. You would use an indicator column for this scenario as well, so that Minitab knows which runs from the original data set were used to create your optimal design. For both “Augment…” and “Evaluate…”, you compare your newly obtained D-Optimality measures to your old ones and see if they have improved.
I hope this information aids you the next time you want to reduce the size of your general full factorial designed experiment!
You might also like:
Gummi Bear DOE: General Full Factorial Designs



