Did you know that tomorrow is World Rabies Day? It’s a day to highlight the impact of human and animal rabies and promote how to stop the disease by combating it in animals first. I found it surprising to learn that more than 55,000 people, mostly in Africa and Asia, die from rabies every year. The global source of most rabies cases in humans is from uncontrolled rabies in dogs, which is spread to humans through a bite. The good news is that rabies in humans can be eliminated by ensuring pets receive rabies vaccinations.
You’re probably thinking "What does rabies have to do with statistics?" Well, while I was scouring the web trying to learn more about rabies (don’t worry, I wasn’t bitten by a rabid dog), I found this mention of confidence intervals (CI) listed in the epidemiology section of a report on rabies from the World Health Organization (WHO):

What is a Confidence Interval?
As blogger Patrick Runkel put it, confidence intervals help you “evaluate the certainty of an estimate.” A CI gives you a bigger picture of the reality, rather than just an average value that might be reported in the news.
A typical use of CI’s in the quality improvement world might occur when an automobile manufacturer is looking to find the average amount of time it takes for an auto assembly line to complete a vehicle. The manufacturer would take a sample of completed vehicles and record the time they spent on the assembly line, and then perform a 1-sample t-test in Minitab to obtain a 95% CI for the mean amount of time all vehicles spend on the line. Because 95% of the CI’s constructed from all possible samples will contain the population parameter (parameter = descriptive measure of an entire population), the manufacturer can conclude with 95% certainty that the mean completion time falls between the CI’s endpoints, or confidence limits.
In statistics, creating confidence intervals is comparable to throwing nets over a target with an unknown, yet fixed, location. Check out the graphic below, which depicts CI’s generated from 20 samples of the same population. The black line represents the fixed value of the unknown population parameter, the population mean; the 19 blue CI’s contain the true value of the population parameter; the 1 red CI does not.
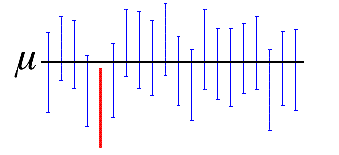
A 95% CI indicates that 19 out of 20 samples (95%) taken from the same population will produce CI’s that contain the true population parameter. A 90% CI indicates that 18 out of 20 samples from the same population will produce CI’s that contain the population parameter, and so on.
So back to the rabies report...it states that the lack of rabies vaccines and lack of awareness of the risks kills more than 55,000 people worldwide each year. And in most news articles, the 55,000 is all that would be listed (this is what I meant above by news articles often listing only the ‘average value’).
However, in this report there is also a CI given – “90% CI = 24,000-93,000.” What the CI is really saying is that you can be 90% confident that the population parameter of worldwide rabies deaths will fall between 24,000 and 93,000. The low and high confidence limits are 24,000 and 93,000, respectively.
Let’s analyze another CI listed in the article:
A 90% CI of between $540.1 million and 626.3 million USD is given after the average annual cost of rabies in Africa and Asia ($583.5 million). The interval in this case ($540.1 – $626.3) provides a good estimate of where the true average will fall. The 90% level of confidence indicates the probability the given range captures the average. In other words, 90% of the observed confidence intervals will hold the true value of the parameter. Keep in mind that the level of confidence is set by the researcher, and is not determined by the data. Also keep in mind that greater levels of confidence give larger CI’s, and thus less precise estimates of the parameter.
While scientific reports that include estimates and averages are more likely to include CI’s because they are geared towards a scientific crowd, remember that CI’s likely exist for the averages given in news articles written for the general public—they just aren’t listed. When reading news articles, it’s helpful to remember that those average values are indeed estimates, with plenty of “wiggle room” on both sides. And this concept of “wiggle room” is demonstrated by the limits of a CI.
For more information about confidence intervals, check out these posts written by my fellow bloggers:
Live Long—And Have Confidence in Your Results
Reaching a Sweet Conclusion with Confidence Intervals



