Une fois que vous avez adapté un modèle linéaire en utilisant l’analyse de régression, l’ANOVA ou les plans d’expériences (DOE), vous devez déterminer dans quelle mesure le modèle s’ajuste aux données. Pour vous aider, le Logiciel statistique Minitab présente une variété de statistiques d’adéquation d’ajustement. Dans cet article, nous allons explorer la statistique R-carré (R² ), certaines de ses limites, et découvrir quelques surprises au passage. Par exemple, les valeurs faibles de R-carré ne sont pas toujours mauvaises et les valeurs R-carré élevées ne sont pas toujours bonnes !
Qu’est-ce que l’adéquation de l’ajustement pour un modèle linéaire ?

Définition : Valeur résiduelle et observée - Valeur ajustée
La régression linéaire calcule une équation qui minimise la distance entre la ligne ajustée et tous les points de données. Techniquement, la régression ordinaire des moindres carrés (OLS) minimise la somme des résidus au carré.
En général, un modèle correspond bien aux données si les différences entre les valeurs observées et les valeurs prévues du modèle sont faibles et non biaisées.
Avant d’examiner les mesures statistiques pour l’adéquation de l’ajustement, vous devriez vérifier les graphiques des valeurs résiduelles. Les graphiques des valeurs résiduelles peuvent révéler des schémas/tendances indésirables qui indiquent des résultats biaisés plus efficacement que les nombres. Lorsque vos graphiques des valeurs résiduelles valident les différentes hypothèses du modèle, vous pouvez faire confiance à vos résultats numériques et vérifier les statistiques d’adéquation d’ajustement
Qu’est-ce que le R-carré ?
Le R-carré est une mesure statistique de la proximité des données à la droite de régression ajustée. Il est également connu sous le nom de coefficient de détermination, ou le coefficient de détermination multiple pour la régression multiple.
La définition du R-carré est assez simple; c’est le pourcentage de variation de la variable de réponse qui est expliqué par un modèle linéaire. Ou:
R-carré = Variation expliquée / Variation totale
Le R-carré est toujours compris entre 0 et 100%:
- 0 % indique que le modèle n’explique aucune de la variabilité des données de réponse autour de sa moyenne.
- 100% indique que le modèle explique toute la variabilité des données de réponse autour de sa moyenne.
En général, plus le R-carré est élevé, meilleur est le modèle qui s’ajuste à vos données. Cependant, il y a des conditions importantes pour cette recommandation dont je vais à la fois parler dans cet article et mon prochain article.
Représentation graphique de R-carré
Tracer des valeurs ajustées en fonction des valeurs observées illustre graphiquement différentes valeurs de R-carré pour les modèles de régression.
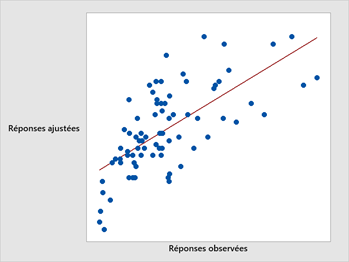

Le modèle de régression à gauche représente 46,1 % de la variance, tandis que celui de droite représente 71,7 %. Plus la variance expliquée par le modèle de régression est importante, plus les points de données se rapprocheront de la ligne de régression ajustée. Théoriquement, si un modèle pouvait expliquer 100% de la variance, les valeurs ajustées seraient toujours égales aux valeurs observées et, par conséquent, tous les points de données tomberaient sur la ligne de régression ajustée.
Prêt(e) pour une démonstration du logiciel d'analyse de données Minitab ? Ecrivez-nous >
Principales limites du R-carré
Le R-carré ne peut déterminer si les estimations des coefficients et les prévisions sont biaisées, c’est pourquoi vous devez évaluer les graphiques des valeurs résiduelles.
Le R-carré n’indique pas si un modèle de régression est adéquat. Vous pouvez avoir une faible valeur R-carré pour un bon modèle, ou une valeur élevée du R-carré pour un modèle qui ne s’ajuste pas aux données!
Le R-carré dans vos résultats est une estimation biaisée du R-carré de la population.
Les valeurs faibles de R-carré sont-elles intrinsèquement mauvaises ?
Non ! Il y a deux raisons principales pour lesquelles il peut être très bien d’avoir de faibles valeurs R-carré.
Dans certains domaines, on s’attend à ce que vos valeurs du R-carré soient faibles. Par exemple, tout domaine qui tente de prédire le comportement humain, comme la psychologie, a généralement des valeurs R-carré inférieures à 50%. Les humains sont tout simplement plus difficiles à prévoir que, disons, les processus physiques.
En outre, si votre valeur R-carré est faible mais que vous avez des prédicteurs statistiquement significatifs, vous pouvez toujours tirer des conclusions importantes sur la façon dont les changements dans les valeurs des prédicteurs sont associés à des changements dans la valeur de réponse. Indépendamment du R-carré, les coefficients significatifs représentent toujours le changement moyen dans la réponse pour une unité de changement dans le prédicteur tout en maintenant les autres prédicteurs dans le modèle constant. De toute évidence, ce type d’information peut être extrêmement précieux.
Un faible R-carré est plus problématique lorsque vous voulez produire des prévisions qui sont raisonnablement précises (qui ont un assez petit intervalle de prévision). Quelle devrait être la valeur du R-carré pour la prévision? Eh bien, cela dépend de vos besoins pour la largeur de l’intervalle de prévision et de la quantité de variabilité présente dans vos données. Bien qu’un R-carré élevé est nécessaire pour des prévisions précises, il n’est pas suffisant en soi, comme nous le verrons.
Les valeurs élevées de R-carré sont-elles intrinsèquement bonnes ?
Non! Un R-carré élevé n’indique pas nécessairement que le modèle a un bon ajustement. Cela pourrait être une surprise, mais observez la courbe ajustée et le graphique des valeurs résiduelles ci-dessous. La courbe ajustée montre la relation entre la mobilité des électrons semi-conducteurs et le logarithme népérien de la densité pour de vraies données expérimentales.

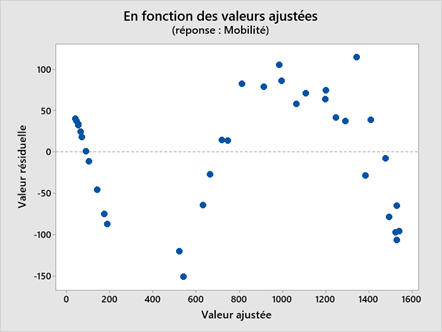
La courbe ajustée montre que ces données suivent une belle fonction cubique et le R-carré est de 98,5%, ce qui semble plutôt bien. Cependant, observez de plus près pour voir comment la courbe de régression va systématiquement sur et sous-prédire les données (biais) à différents points le long de la courbe. Vous pouvez également voir les tendances dans les valeurs résiduelles en fonction des valeurs ajustées, plutôt que le caractère aléatoire que vous voulez observer. Cela indique un mauvais ajustement, et sert de rappel quant à pourquoi vous devriez toujours vérifier les graphiques des valeurs résiduelles.
Cet exemple vient de mon article sur le choix entre régression linéaire et non linéaire. Dans ce cas, la réponse consiste à utiliser la régression non linéaire parce que les modèles linéaires ne sont pas en mesure de s’adapter à la courbe spécifique que ces données suivent.
Cependant, des biais similaires peuvent se produire lorsque votre modèle linéaire n’inclut pas des prédicteurs importants, des termes polynomiaux et des termes d’interaction. Les statisticiens appellent cela le biais de spécification, et il est causé par un modèle sous-spécifié. Pour ce type de biais, vous pouvez corriger les résidus en ajoutant les termes appropriés au modèle.
Pour plus d’informations sur la façon dont un R-carré élevé n’est pas toujours une bonne chose, lisez mon article Cinq raisons pour lesquelles votre R-carré peut être trop élevé.
Réflexions finales sur le R-carré
Le R-carré est une mesure pratique, apparemment intuitive de la façon dont votre modèle linéaire s’ajuste à un ensemble d’observations. Cependant, comme nous l’avons vu, le R-carré ne nous raconte pas toute l’histoire. Vous devez évaluer les valeurs R-carré en conjonction avec les valeurs résiduelles, d’autres statistiques du modèle, et la connaissance pratique/physique du sujet afin de compléter l’histoire.
Bien que le R-carré fournit une estimation de la force de la relation entre votre modèle et la variable de réponse, il ne fournit pas un test d’hypothèse formel pour cette relation. Le Test F d’importance globale détermine si cette relation est statistiquement significative.
Dans mon prochain article, nous allons continuer sur le thème que le R-carré par lui-même est incomplet et voir deux autres types de R-carré: R-carré ajusté et R-carré prévu. Ces deux mesures permettent de surmonter des problèmes spécifiques afin de fournir des informations supplémentaires vous permettant d’évaluer la puissance explicative de votre modèle de régression.
Pour en savoir plus sur le R-carré, découvrez la réponse à cette question éternelle : Quelle devrait être la valeur minimum du R-carré ?
Découvrez et essayez gratuitement la version d'essai du logiciel d'analyse de données Minitab >



