Dans de nombreuses industries, en particulier la production et dans la chaîne logistique automobile, la taille d'échantillon standard pour les études de capabilité est de 30 pièces.
Comme tout calcul statistique, la taille de l'échantillon a un effet inverse sur l'erreur. À mesure que la taille de l'échantillon augmente, l'erreur diminue. Alors que nous évaluons la capabilité d'un processus, nous voulons que l'erreur soit minimisée et, par conséquent, nous souhaiterions sans doute une taille d'échantillon plus grande.

Quelles sont les raisons pour réaliser une étude de capabilité ?
Il y a trois raisons :
- Pour évaluer le comportement du procédé - est-il stable / prévisible (« sous contrôle ») ou est-il instable / imprévisible (hors de contrôle) ?
- Évaluer à la fois les performances réelles du procédé par rapport à la spécification ainsi que son potentiel à produire des pièces dans les spécifications à l'avenir
- Pour déterminer combien de pièces hors spécifications le procédé est susceptible de produire.
D’où vient cette règle des 30 ?
De nombreuses personnes utilisent 30 pièces comme seuil d’échantillonnage. Cela est dû à l’idée fausse que pour qu’une analyse soit « statistiquement significative », elle a besoin d’un échantillon de 30 pièces.
Ainsi, « 30 » est devenu le nombre quelque peu arbitraire que les gens ont tendance à considérer comme assez grand pour effectuer une analyse de capabilité. S'il est vrai que le nombre 30 a un rôle dans les statistiques, en particulier avec la distribution t, il n'y a pas de relation entre ce nombre et la capabilité d'évaluer correctement le comportement d'un procédé et sa capabilité à respecter les spécifications.
Comme le montre l’exemple présenté, le nombre 30 est insuffisant pour modéliser correctement le procédé.
Le saviez-vous : dans l'industrie automobile, c'est en fait une règle de 100 !
Par exemple, dans leurs manuels de Contrôle Statistiques des Procédés (SPC) et Production Part Approval Process (PPAP) publiés par le Groupe d’Action de l’Industrie Automobile Automotive Industry Action Group (AIAG), 100 pièces est défini comme la taille d'échantillon appropriée pour une étude de capabilité initiale (basée sur 20 sous-groupes de cinq ou 25 sous-groupes de quatre). Cependant, chaque processus est différent, donc le nombre « correct » de votre processus dépend de ses sources de variation.
Alors quel échantillon devez-vous prendre en considération, 30 ou 100 pièces ?
Contrairement à la conception d'expériences ou de tests d'hypothèses, les études de capabilité ne portent pas sur la puissance statistique, mais sur la variabilité. Ai-je correctement saisi toutes les variations (ou les sources les plus importantes) de mon procédé dans mon étude ? Quel que soit le nombre d'échantillons que vous prélevez, en utilisant des intervalles de confiance dans votre analyse de capabilité, vous pouvez obtenir une plage de l'emplacement de la véritable capabilité. Un intervalle trop large peut être un indicateur que votre échantillon était tout simplement trop petit.
Par exemple, supposons que nous ayons une population théorique (10 000) à partir d'une distribution normale qui a une moyenne de 30 mm et un écart-type de 1 mm. Avec une spécification inférieure de 25 mm et une spécification supérieure de 35 mm, nous pouvons savoir que la « vraie » capabilité (nous utiliserons Pp pour plus de simplicité) est de 1,67 :
𝑃𝑝= ((𝑈𝑆𝐿−𝐿𝑆𝐿))/6𝑠=((35−25))/((6×1))=10/6=1.67
Dans Minitab, comme vous pouvez le voir, en utilisant l'ensemble de notre population, nous obtenons un PP de 1,67, ce qui est exactement ce à quoi nous nous attendions.
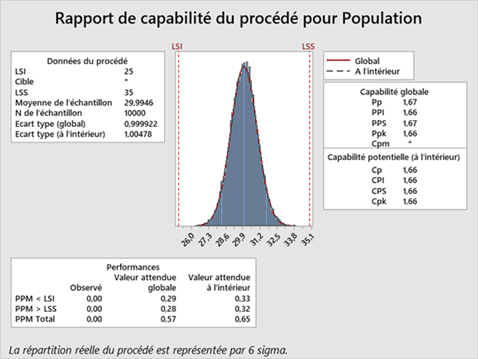
Voyons maintenant le Pp que nous obtenons lorsque nous échantillonnons cette population :
Scénario 1 : W échantillonner cette population 100 fois avec n = 30 et donner la plage des Pp calculés
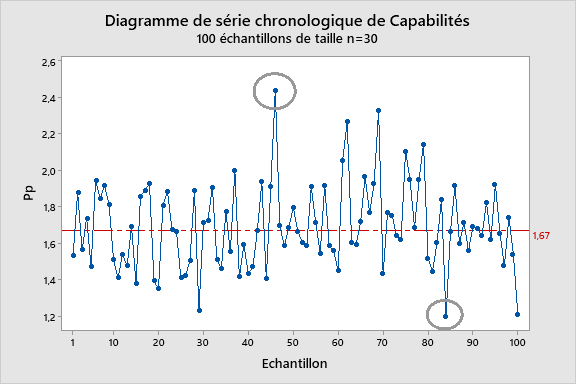
Maintenant, si nous échantillonnons nos données 100 fois, en utilisant 30 pièces, vous remarquerez dans le graphique ci-dessous que nous obtenons une énorme variabilité. Globalement, notre Pp moyen était de 1,69, ce qui est proche de la « vraie » valeur, mais nos échantillons variaient entre un minimum de 1,19 et un maximum de 2,44.
En effet, nous avons eu beaucoup de variabilité dans les résultats de notre échantillon de 30 pièces, avec des Pps à la fois significativement inférieurs et supérieurs aux Pp des populations réelles.
En utilisant uniquement cette taille d'échantillon, nous pourrions arriver à une conclusion erronée.
Alors, comment s'assurer que nous nous rapprochons du bon PP ?
Une bonne pratique pour capturer la fiabilité de notre estimation de Pp consiste à utiliser les intervalles de confiance de Minitab, disponibles dans Stat> Outils de la Qualité> Analyse de capabilité> Options. Nous avons échantillonné le processus une fois, en utilisant 30 points de données, et activé les intervalles de confiance et obtenu le résultat suivant :
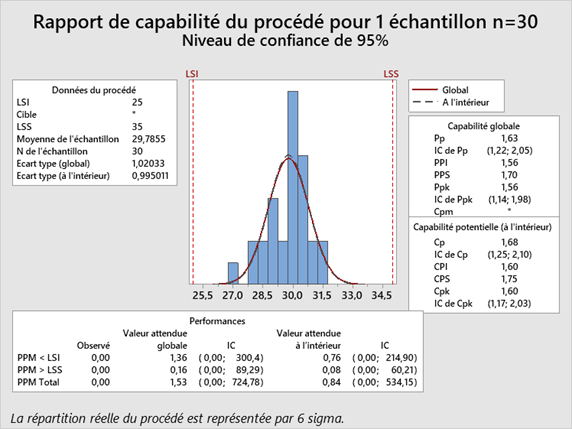
Comme vous pouvez le voir, sur la base de l'échantillon de 30 pièces, nous avons obtenu un Pp de 1,63, assez proche de la valeur réelle de 1,67 de la population. En ne regardant que ce nombre, nous pensons que notre processus est capable.
Cependant, en utilisant un intervalle de confiance à 95%, nous nous rapprochons assez des valeurs minimum et maximum que nous avons vues lorsque nous avons exécuté un échantillon de 30 pièces 100 fois.
En d'autres termes, nous obtenons un vrai sens de la variance dans le processus.
Si cet écart est hors spécifications, nous devons vérifier notre processus pour réduire la variabilité.
Conclusion
En général, des échantillons plus importants donneront une bien meilleure estimation de la capabilité réelle.
Les manuels AIAG SPC et PPAP recommandent au moins 100 échantillons. Parfois, la collecte d'échantillons peut être difficile ou coûteuse. Quoi qu'il en soit, en utilisant les intervalles de confiance de Minitab, vous aurez une meilleure idée de la variabilité et éviterez les erreurs coûteuses qui pourraient survenir en raison d'une petite taille d'échantillon.



