Les dispositifs de mesure doivent être calibrés régulièrement pour garantir qu'ils remplissent correctement leur fonction. Si le calibrage couvre un large éventail d'applications et de scénarios, l'objectif est simple : veiller à ce que votre dispositif effectue des mesures conformes à vos normes. La plupart des systèmes de qualité exigent un système de mesure satisfaisant qui comprend un calibrage formel, périodique et documenté de tous les instruments de mesure. Mais les ingénieurs ont souvent du mal à vérifier que deux instruments mesurent des pièces de manière similaire.
COMMENT DÉTERMINER SI DEUX INSTRUMENTS FOURNISSENT DES MESURES COMPARABLES ?
Une approche consiste à comparer les deux instruments en ajustant une droite de régression linéaire simple, puis à utiliser l'ajustement du modèle pour voir si les valeurs sont les mêmes sur toute la plage de mesures. La régression linéaire simple modélise la relation linéaire entre deux variables continues : une réponse et un prédicteur.
EXEMPLE :
Supposons qu'un fabricant de dispositifs médicaux veuille déterminer si son tensiomètre est équivalent à un modèle similaire sur le marché. Pour vérifier que les deux instruments fournissent des mesures comparables, le fabricant sélectionne des personnes qui représentent une plage de valeurs où les mesures doivent être comparables. Ensuite, il prend la tension des personnes avec les deux instruments. La société obtient des mesures de tension artérielle systolique sur un échantillon aléatoire de 60 personnes en utilisant les deux instruments et enregistre les données. Voici un échantillon des 60 lignes, où chaque ligne représente une mesure effectuée à l'aide des instruments actuel et nouveau.
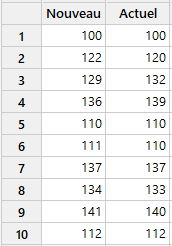
Dans ce cas, nous désignons les mesures du dispositif actuel comme le prédicteur (ou variable X) et les mesures du nouveau dispositif comme la réponse (ou variable Y). L'ajustement d'une droite de régression à ces données montre que les valeurs du dispositif de mesure actuel prédisent assez bien les valeurs du nouveau dispositif de mesure. La statistique R-carré indique que le dispositif de mesure actuel explique 98,8 % de la variation observée dans le nouveau dispositif de mesure.
L'équation de régression est la suivante : Nouveau = 1,387 + 0,9894 Actuel

Il ressort de ces données que les mesures du dispositif actuel peuvent certainement prédire assez bien les mesures du nouveau dispositif. Dans la pratique, nous voyons des ingénieurs utiliser des modèles prédictifs pour vérifier qu'un nouveau dispositif peut effectuer des mesures aussi précises qu'un dispositif actuel. Il existe également d'autres applications, car certaines situations nécessitent une mesure plus rapide. Par exemple, certaines pièces ou certains échantillons doivent être mesurés en laboratoire avant de pouvoir être expédiés. Mais les mesures en laboratoire peuvent prendre des heures, compte tenu du processus. Une méthode de mesure qui fournit des résultats immédiats peut être utilisée pour prédire les mesures en laboratoire, ce qui permet aux opérateurs et aux ingénieurs d'être immédiatement informés des problèmes potentiels.
L'approche de régression linéaire simple est efficace à condition de pouvoir supposer qu'il n'y a pas d'erreurs dans la direction horizontale ou X. Dans cet exemple, cela suppose que notre système de mesure actuel ne contient aucune erreur. Dans le cas des systèmes de mesure, nous savons que cette hypothèse n'est pas raisonnable et que l'utilisation d'une régression linéaire simple n'est donc pas la meilleure approche statistique. Mais rassurez-vous, il existe une autre approche tout aussi facile à utiliser.
Familiarisez-vous avec une large gamme d'outils graphiques et statistiques
lors de l'une de nos sessions de formation virtuelles
QU'EST-CE QUE LA RÉGRESSION ORTHOGONALE ?
La régression orthogonale, également appelée régression de Deming, peut être utilisée pour déterminer si deux instruments ou méthodes fournissent des mesures comparables. La régression orthogonale examine également la relation linéaire entre deux variables continues : une réponse (Y) et un prédicteur (X). Contrairement à la régression linéaire simple (régression par les moindres carrés), la réponse et le prédicteur dans la régression orthogonale contiennent tous deux une erreur de mesure. Rappelons que dans une régression simple, seule la variable de réponse contient une erreur de mesure. Si vous utilisez la régression simple pour déterminer la comparabilité lorsque les deux variables contiennent une erreur de mesure, les résultats dépendent de la variable que les calculs supposent sans erreur de mesure. La régression orthogonale résout ce problème, si bien que le rôle des variables a peu d'influence sur les résultats.
Dans une régression linéaire simple, l'objectif est de minimiser la somme des carrés des distances verticales entre les valeurs y et les valeurs correspondantes sur la droite d’ajustement. Dans la régression orthogonale, l'objectif est de minimiser les distances orthogonales (perpendiculaires) entre les points de données et la droite d'ajustement. Bien que la différence entre ces approches puisse sembler mineure, lors de l'évaluation des mesures et des pièces par rapport aux spécifications, elle pourrait donner lieu à des conclusions bien différentes.
Analysons les données du tensiomètre en utilisant la régression orthogonale.
La régression orthogonale exige de spécifier le rapport de la variance de l'erreur pour X (Actuel) et Y (Nouveau). Lorsque la méthode de mesure de X et Y est la même, les variances sont susceptibles d'être égales, ce qui donnerait un rapport égal à 1. Mais la bonne pratique consiste à l'estimer. Avant la collecte des données pour la régression orthogonale, les ingénieurs ont effectué des études séparées sur chaque tensiomètre pour estimer la variation des mesures. Le rapport des variances des erreurs a été calculé en effectuant une étude indépendante de répétabilité et de reproductibilité de l'instrumentation pour chaque dispositif de mesure afin de générer une composante de variance pour la répétabilité de chaque dispositif. Le rapport des deux composantes de variance pour les estimations de la répétabilité peut être utilisé comme entrée pour le champ du rapport des variances des erreurs. La variance pour le nouveau tensiomètre était de 1,08. La variance pour le tensiomètre de l'autre société était de 1,2. L'ingénieur décide d'affecter le nouveau tensiomètre à la variable de réponse et le tensiomètre actuel de l'autre société à la variable de prédiction. Avec ces affectations, le rapport de variance des erreurs est de 1,08 / 1,2 = 0,9.

RÉSULTATS DE LA RÉGRESSION ORTHOGONALE
La droite d'ajustement montre que les points sont proches de la droite de régression, ce qui indique que le modèle s'adapte aux données. Nous présentons ici l'ajustement par les moindres carrés et l'ajustement orthogonal. Les deux équations d'ajustement sont visibles en bas à gauche du visuel.
Notez que même si les droites semblent très similaires, l'équation de régression orthogonale est différente de l'équation de régression linéaire simple. Nous pouvons utiliser l'équation de régression orthogonale pour comprendre l'équivalence des deux instruments de mesure.
Si l'une des conditions suivantes est vérifiée, les résultats fournissent la preuve que les tensiomètres ne sont pas équivalents :
- L'intervalle de confiance pour la pente ne contient pas 1.
- L'intervalle de confiance pour la constante ne contient pas 0.

Habituellement, un niveau de confiance de 95 % suffit. Un niveau de confiance de 95 % indique que, si vous preniez 100 échantillons aléatoires de la population, les intervalles de confiance d'environ 95 des échantillons contiendraient la vraie valeur du coefficient. Pour un ensemble de données défini, un niveau de confiance plus faible produit un intervalle plus étroit, et un niveau de confiance plus élevé produit un intervalle plus large.
Les résultats montrent que l'intervalle de confiance pour la constante, qui est d'environ -2,78 à 4,06, contient 0. L'intervalle de confiance pour la pente, Courant, qui est d'environ 0,97 à 1,02, contient 1. Ces résultats ne fournissent pas la preuve que les mesures des tensiomètres diffèrent. Sur la base de ces résultats, la société peut conclure que son nouveau dispositif de mesure est aussi performant que le dispositif actuellement disponible sur le marché.
CONCLUSION
Lors du calibrage de deux systèmes de mesure, la régression orthogonale peut permettre de déterminer si les instruments ou les méthodes fournissent des mesures comparables. Contrairement à la régression linéaire simple (également appelée régression par les moindres carrés), la réponse et le prédicteur dans la régression orthogonale contiennent tous deux une erreur de mesure. En utilisant la régression orthogonale, le fabricant de dispositifs médicaux peut conclure en toute confiance que son instrument de mesure est équivalent à l'instrument de mesure actuellement disponible sur le marché.
La fonction de régression orthogonale est disponible dans la plupart des logiciels de statistiques, y compris Minitab Statistical Software.
Téléchargez une version d'essai gratuite de Minitab Statistical Software





