10月、MLBの勝ち残ったチームがワールドシリーズをめざして戦い、佳境を迎えています。 野球ファンにとっては興奮する季節であり、同じぐらい統計に熱くなっている人にとっては、野球データを分析するのにもってこいの季節です！このブログでは、2つの密に関連する分析を切り離してみます。Minitab Statistical Softwareで簡単にできる分析、分散分析（ANOVA）と平均の分析（ANOM）です。「どの野球場が打者に適し、どの野球場が投手に適しているか？」に答えることで、2つの分析の違いを説明します。
私のデータは、ESPNのMLB野球場因子から得た、2001年～現在のものです。まず、この分析に注意が必要な理由を説明します。
- ホワイトソックス、カブス、アスレチックスの野球場を省いていることを、このチームのファンにお詫びいたします。ESPNのデータには、シカゴのどの野球場がどのチームのものかが書いていないのです。
- 1960年代からずっと同じ野球場でプレーしているにもかかわらず、アスレチックスのデータは2年分しかありませんでした。
- ESPNは、ヒットの種類ごとに野球場因子を出しているため、データを使用して、単打に最適な野球場、ホームランに最適な野球場などを割り出すことができます。各野球場の得点数に基づくデータのみを使用していきます。
ANOVAとANOM分析の追記
本題に入る前に、ちょっとお話ししたい点があります。ANOVAとANOMは、母集団のランダムな標本を使用して、標本の結果をより大きな母集団に一般化する分析です。年ごとのデータがランダムな標本を表しているとは考えにくいので、この分析をまじめな推論とはとらえないでください。それでも、結果は、2つの分析が答える質問の違いを示すのに役立ちます。
分析のスキルセットを強化し、データに関する専門知識をさらに高める準備はできていますか？
ANOVA分析の帰無仮説は、比較グループの平均がすべて互いに等しいというものです。ANOVA分析に多重比較が含まれることが多いです。多重比較では、グループの平均の間の差を調べて、統計的にどの平均がどの程度異なるかを割り出します。
ANOMの帰無仮説は、すべてのグループ平均がすべてのデータの平均に等しいというものです。ANOMの帰無仮説が真であれば、ANOVAの帰無仮説も真です。分析目標に違いが現れて帰無仮説を棄却するときです。
野球場分析#1 一元配置分散分析（ANOVA）を使用する
最初の分析では、一元配置分散分析（ANOVA）検定を使用します。関心の比較を選択することで、この種の分析をさらに深く掘り下げることができます。 ここでは、すべての野球場を、最も得点の少なかった野球場、ペトコ・パークと比較しています。
もう少し見てみますか？こちらが、分析したデータセットを含むMinitab 20.4プロジェクトです。野球場の名前の前に野球場因子ランクを追加したので、このデータセットは特別です。この追加により、Minitabで結果の野球場名をアルファベット順に並べると、最小因子から最大因子の順に並びます。
- [統計] > [ANOVA] > [一元]を選択します。
- [応答]で、得点を入力します。
- [因子]で、「野球場名」を入力します。
- [比較]をクリックします。
- [HsuのMCB]を選択します。
- [特性]で、[最小特性]を選択します。
- 各ダイアログで、[OK]をクリックします。
上の結果には、どの野球場がペトコ・パークより打者向きかが示されています。このリストには、19か所の野球場が記載されており、デンバーのクアーズ・フィールドも入っています。デンバーの標高が打者に適した環境であることはよく知られています。
このANOVA情報はとても役に立ちます。ペトコ・パークよりも打者向きの野球場、そしてペトコ・パークと大差ない野球場を見ることができます。多重比較の異なるセットにすることで、それぞれの野球場を他のそれぞれの野球場と比較したり、それぞれの野球場を選択した1か所の野球場と比較したりできます。グループ間の差が主な
焦点です。ANOMで、別の質問に答えます。野球場を、打者の野球場、中立の野球場、投手の野球場に分類するにはどうしたらいいでしょうか？
グラフの点は、平均野球場因子です。中心線は、全平均です。外側の線は、どの野球場が全平均と異なるかを示す決定限界です。
30日間のMinitab Statistical Softwareトライアル版をダウンロードしましょう！
野球場分析#2 平均の分析（ANOM）を使用する
ANOMでは、平均が互いに等しいかを検定するのではなく、平均が全平均に等しいかを検定します。Minitabでは、結果がわかりやすくなるよう、グラフが作成されます。同じデータセットで以下の手順を実行して、結果を得ることができます。
- [統計] > [ANOVA] > [平均の分析]を選択します。
- [応答]で、得点を入力します。
- [因子1]の[通常]に、「野球場名」を入力します。
- [OK]をクリックします。
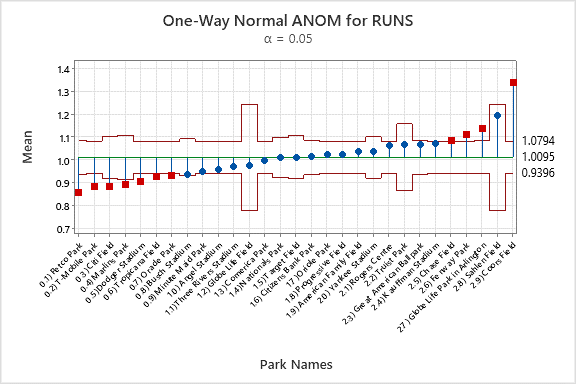グラフの点は、平均野球場因子です。中心線は、全平均です。外側の線は、どの野球場が全平均と異なるかを示す決定限界です。 | このデータに含まれている7か所の投手の野球場： | および4か所の打者の野球場： |
|
|
統計分析で意思決定が向上
応用するにあたり、正しい質問に答える分析を使用することは、適切な意思決定を行うための鍵です。ANOVAとANOMの違いに注意してください。
ANOVAでは、以下の2つのカテゴリがあります。
- ペトコ・パークと大差ない
- ペトコ・パークより打者向き
ANOMでは、以下の3つのカテゴリがあります。
- 全平均より低い
- 全平均と大差ない
- 全平均より高い
カテゴリ分けにも違いがあることに注意してください。ANOVA分析では、ブッシュ・スタジアムは、ペトコ・パークと大差ないため、投手に有利な野球場と考えるでしょう。ANOM分析では、ブッシュ・スタジアムは、全平均と大差ないため、得点については中立的な野球場と考えるでしょう。ANOVA分析では、19か所の野球場がペトコ・パークよりも打者向きであることがわかりました。ANOM分析では、4か所の野球場が全平均よりも打者向きであることがわかりました。
分析の力の詳細は、以下の関連ブログをご覧ください。
ANOMのセーレン・フィールドの部分は興味深いです。セーレン・フィールドには打者の野球場のように見える平均があるにもかかわらず、統計的には打者の野球場に分類されていません。ここで、トロント・ブルージェイズは2シーズンしかゲームをプレーしていません。このデータがランダムな標本である場合、データの変動が大きすぎ、標本が小さすぎて、セーレン・フィールドがいつでも打者向きの野球場であるという統計的証拠を出せないことがわかります。平均とグループ内変動間の差の関係は、データの変動を考慮する統計分析を使用する上で、重要な利点です。
ANOVAやANOMのような統計分析で得られる洞察により、データ（この場合は野球場）を元により良い意思決定を行うことができます。グループを比較した結果を活用して、自分の生活やあらゆる業界のほぼすべての役割でより良い意思決定を行う方法はたくさんあります。別の事例でグループを比較した結果として、Riverview病院協会が特定の患者グループを識別した方法をご参照ください。ある患者グループの満足度が他のグループよりも低く、その改善プロセスを適切に協会が実行しているものです。