--- title: ワイブル分布がいつでも歓迎されるのはなぜか? Why the Weibull Distribution Is Always Welcome? description: ワイブル分布がいつでも歓迎されるのはなぜか image: https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/prob_dist_plots_dialog-Jul-05-2025-10-42-05-8953-PM.gif --- 日本語 - [English](https://blog.minitab.com/en/?hsLang=ja) - [Français](https://blog.minitab.com/fr/?hsLang=ja) - [Deutsch](https://blog.minitab.com/de/?hsLang=ja) - [Português](https://blog.minitab.com/pt/?hsLang=ja) - [Español](https://blog.minitab.com/es/?hsLang=ja) - [日本語](https://blog.minitab.com/ja/?hsLang=ja) - [한국어](https://blog.minitab.com/ko/?hsLang=ja) - [中文（简体）](https://blog.minitab.com/zh/?hsLang=ja) - [日本語](https://blog.minitab.com/ja/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [Chinese](https://blog.minitab.com/zh/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [Deutsch](https://blog.minitab.com/de/blog/darum-ist-die-weibull-verteilung-überall-willkommen) - [English](https://blog.minitab.com/en/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [Français](https://blog.minitab.com/fr/blog/pourquoi-la-loi-de-weibull-est-elle-souvent-la-plus-utile-explications) - [한국어](https://blog.minitab.com/ko/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [![Icon Partners](https://blog.minitab.com/hubfs/WCM/Partners.png) パートナー](https://www.minitab.com/ja-jp/company/partners/) - [![Icon Contact](https://blog.minitab.com/hubfs/WCM/Contact.png) お問い合わせ窓口](https://www.minitab.com/ja-jp/company/contact-us/) - [![Icon Talk to Minitab](https://blog.minitab.com/hubfs/WCM/Phone.png) Minitabと話す](https://www.minitab.com/ja-jp/talk-to-minitab/) - [![Icon My Account](https://blog.minitab.com/hubfs/WCM/MyAcct.png) マイ アカウント](https://licensing.minitab.com/account/manage) [![Minitab](https://blog.minitab.com/hubfs/WCM/minitab-corp-logo.svg)](https://www.minitab.com/ja-jp/) - 製品 戻る [製品](https://www.minitab.com/ja-jp/products/) [すべての製品](https://www.minitab.com/ja-jp/products/) - [Minitab Solution Center](https://www.minitab.com/ja-jp/products/minitab-solution-center/) - [Minitab Statistical Software](https://www.minitab.com/ja-jp/products/minitab/) - [Minitab Connect](https://www.minitab.com/ja-jp/products/connect/) - [Minitab Model Ops](https://www.minitab.com/ja-jp/products/model-ops/) - [Minitab Education Hub](https://www.minitab.com/ja-jp/products/education-hub/) - [Minitab Engage](https://www.minitab.com/ja-jp/products/engage/) - [Minitab Workspace](https://www.minitab.com/ja-jp/products/workspace/) - [Real-Time SPC](https://www.minitab.com/ja-jp/products/real-time-spc/) - [Prolinkデータ収集およびSPC](https://info.minitab.com/ja/shop-floor-connectivity-with-prolink?hsLang=ja) - [Simul8離散事象シミュレーション](https://info.minitab.com/ja/new-to-simul8?hsLang=ja) - [SPM](https://www.minitab.com/ja-jp/products/spm/) - ソリューション 戻る [ソリューション](https://www.minitab.com/ja-jp/solutions/) [すべてのソリューション](https://www.minitab.com/ja-jp/solutions/) - [分析](https://www.minitab.com/ja-jp/solutions/analytics/) - [統計・予測分析](https://www.minitab.com/ja-jp/solutions/analytics/statistical-analysis-predictive-analytics/) - [データ科学・機械学習](https://www.minitab.com/ja-jp/solutions/analytics/data-science-machine-learning/) - [ビジネス分析・インテリジェンス](https://www.minitab.com/ja-jp/solutions/analytics/business-analytics-intelligence/) - [統計的工程管理](https://www.minitab.com/ja-jp/solutions/analytics/statistical-process-control/) - [運営・品質分析](https://www.minitab.com/ja-jp/solutions/analytics/quality-analytics/) - [Live Analytics](https://www.minitab.com/ja-jp/solutions/analytics/live-analytics/) - [信頼性 & 寿命データ分析](https://www.minitab.com/ja-jp/solutions/analytics/reliability/) - [ディスクリートイベントシミュレーション](https://info.minitab.com/ja/new-to-simul8?hsLang=ja) - [プロセスマイニング](https://info.minitab.com/ja/new-to-simul8?hsLang=ja) - [重要な能力](https://www.minitab.com/ja-jp/solutions/key-capabilities/) - [継続的改善](https://www.minitab.com/ja-jp/solutions/key-capabilities/continuous-improvement/) - [データ統合とデータ準備](https://www.minitab.com/ja-jp/solutions/key-capabilities/data-integration-data-prep/) - [ダイアグラム作成とマインドマップ作成](https://www.minitab.com/ja-jp/solutions/key-capabilities/diagramming-mind-mapping/) - [モデル展開とML Ops](https://www.minitab.com/ja-jp/solutions/key-capabilities/model-deployment-ml-ops/) - [イノベーションおよびプロジェクト管理](https://www.minitab.com/ja-jp/solutions/key-capabilities/innovation-project-management/) - [プロセスエクセレンス：検出、修正、および防止](https://www.minitab.com/ja-jp/solutions/key-capabilities/process-excellence/) - [自動データ収集](https://info.minitab.com/ja/shop-floor-connectivity-with-prolink?hsLang=ja) - [産業ソリューション](https://www.minitab.com/ja-jp/solutions/industry/) - [アカデミック](https://www.minitab.com/ja-jp/solutions/industry/academic/) - [エネルギー・天然資源](https://www.minitab.com/ja-jp/solutions/industry/energy-resources/) - [政府・公共部門](https://www.minitab.com/ja-jp/solutions/industry/government/) - [医療](https://www.minitab.com/ja-jp/solutions/industry/healthcare/) - [保険](https://www.minitab.com/ja-jp/solutions/industry/insurance/) - [製造産業](https://www.minitab.com/ja-jp/solutions/industry/manufacturing-industrial/) - [サービス](https://www.minitab.com/ja-jp/solutions/industry/service-industries/) - [ソフトウェアとテクノロジー](https://www.minitab.com/ja-jp/solutions/industry/software-technology/) - [建設](https://www.minitab.com/ja-jp/solutions/industry/construction/) - [機能/役割](https://www.minitab.com/ja-jp/solutions/role/) - [エンジニアリング](https://www.minitab.com/ja-jp/solutions/role/engineering/) - [ビジネス分析](https://www.minitab.com/ja-jp/solutions/role/business-analysts/) - [情報技術](https://www.minitab.com/ja-jp/solutions/role/information-technology/) - [サプライチェーン](https://www.minitab.com/ja-jp/solutions/role/supply-chain/) - [カスタマーサービスソリューション](https://www.minitab.com/ja-jp/solutions/role/customer-service-contact-center/) - [人事](https://www.minitab.com/ja-jp/solutions/role/human-resources/) - [マーケティングデータ分析](https://www.minitab.com/ja-jp/solutions/role/marketing/) - [研究開発](https://www.minitab.com/ja-jp/solutions/role/research-and-development/) - リソースとサービス 戻る [リソースとサービス](https://www.minitab.com/ja-jp/resources-services/) [全リソースとサービス](https://www.minitab.com/ja-jp/resources-services/) - [リソース](https://www.minitab.com/ja-jp/resources-services/resources/) - [ケーススタディ](https://www.minitab.com/ja-jp/resources-services/resources/case-studies/) - [ブログ](https://www.minitab.com/ja-jp/resources-services/resources/blog/) - [データセット](https://www.minitab.com/ja-jp/resources-services/resources/data-set/) - [ウェビナーとイベント](https://www.minitab.com/ja-jp/resources-services/resources/events/) - [Education Hub](https://www.minitab.com/ja-jp/resources-services/resources/education-hub/) - [サービス](https://www.minitab.com/ja-jp/resources-services/services/) - [トレーニング](https://www.minitab.com/ja-jp/resources-services/services/training/) - [展開](https://www.minitab.com/ja-jp/resources-services/services/deployment/) - [統計コンサルティング](https://www.minitab.com/ja-jp/resources-services/services/statistical-consulting/) - [自習型学習](https://www.minitab.com/ja-jp/resources-services/services/self-paced-learning/) - [社会人教育](https://www.minitab.com/ja-jp/resources-services/services/continuing-education/) - サポート 戻る [サポート](https://www.minitab.com/ja-jp/support/) [技術サポート](https://www.minitab.com/ja-jp/support/) - [サブスクリプションとアクティベーション](https://www.minitab.com/ja-jp/support/subscriptions-and-activation/) - [Minitab Quick Start](https://www.minitab.com/ja-jp/support/quick-start/) - [トレーニング](https://www.minitab.com/ja-jp/resources-services/services/training/) - [インストールのサポート](https://www.minitab.com/ja-jp/support/installation/) - [サポート動画](https://www.minitab.com/ja-jp/support/videos/) - [ソフトウェアドキュメント](https://www.minitab.com/ja-jp/support/documents/) - [ソフトウェアの更新](https://www.minitab.com/ja-jp/support/software-updates/) - [製品のダウンロード](https://www.minitab.com/ja-jp/support/downloads/) - [サポートポリシー](https://www.minitab.com/ja-jp/support/policy/) - 会社 戻る [会社](https://www.minitab.com/ja-jp/company/) [会社](https://www.minitab.com/ja-jp/company/) - [企業情報](https://www.minitab.com/ja-jp/company/our-company/) - [リーダーチーム](https://www.minitab.com/ja-jp/company/leadership-team/) - [パートナー](https://www.minitab.com/ja-jp/company/partners/) - [採用情報](https://www.minitab.com/ja-jp/company/careers/) - [お問い合わせ窓口](https://www.minitab.com/ja-jp/company/contact-us/) - [ニュース](https://www.minitab.com/ja-jp/company/press-releases/) [試用/購入](https://www.minitab.com/ja-jp/try-buy/) - [ブログ無料メルマガへ登録](https://info.minitab.com/ja/blog/subscribe?hsLang=ja) ![Minitab](https://20853177.fs1.hubspotusercontent-na1.net/hubfs/20853177/minitab-corp-logo.svg?t=1755011311618) ## 通知 minitab.com を終了します。 \[続行\] をクリックして次の手順に進みます : 続行 戻る # ワイブル分布がいつでも歓迎されるのはなぜか? Why the Weibull Distribution Is Always Welcome? Minitab Blog Editor | 1/12/2022 トピック: [Reliability Analysis](https://blog.minitab.com/ja/blog/tag/reliability-analysis) - [Share](https://www.linkedin.com/shareArticle?mini=true&url=https://blog.minitab.com/ja/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [Share](https://www.facebook.com/sharer.php?u=https://blog.minitab.com/ja/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) 大学時代、どこへでも出かけ、なじんでしまう友人がいました。教授グループと昼食を取り、公園でヒッピーとフットバッグをし、夜には街一番の硬派なバーで地元のバイカー仲間と遊んでいました。次の日になると、寄せ集めサッカーをし、その後は一晩中ゲーマー仲間とLANパーティーをしていました。週末は大抵、キャンパスでストレートエッジ パンクロッカーの小さなグループと一緒に年齢無制限のショーを見たり、街の仲間とビールパーティーをしたりし、さらに物理学クラブの友だちとダンジョンズ・ドラゴンズゲームをして締めくくっていました。 カメレオンのごとく、一緒にいる人の特徴に自分自身を一致させ、反映することができました。この柔軟性ゆえに、多種多様な社会的環境で歓迎されました。 この友人の名前はJeff Weibull。人気者だったため、この友人にちなんで、地元の統計家が「ワイブル分布」と名付けました。   ## ワイブル分布の人気が高いのはなぜ  上の話の最後の部分は作り話です。Jeffの姓は実は「Weibull」などではありませんし、分布は[違う誰か](https://ja.wikipedia.org/wiki/%E3%83%AF%E3%83%AD%E3%83%83%E3%83%87%E3%82%A3%E3%83%BB%E3%83%AF%E3%82%A4%E3%83%96%E3%83%AB)の名前にちなんだものです。 とはいえ、私はワイブル分布のことを初めて知ったとき、すぐに、Jeffと、どんな社会的環境でも居心地良さそうに見えるその適応力が頭に浮かんだのです。 Jeffが多種多様な社会的環境のカメレオンであったように、ワイブル分布も多種多様な分布の特性を受け入れることができます。このため、エンジニアや品質提供者の間で人気が高まり、信頼性データのモデル化で一番使用される分布になりました。さまざまなデータセットをモデル化できる十分な柔軟性があるため、ワイブル分布をデータ分析に組み込むことを好みます。 データが右に歪んでいますか？Weibullならモデル化できます。データが左に歪んでいますか？Weibullならそれは問題になりません。データが対称になっていますか？Weibullが得意とするところです。エンジニアがワイブル分布を使用して、真空管やコンデンサから玉軸受やリレーまで、あらゆるものの信頼性と材料強度を評価する理由は、この柔軟性です。 ワイブル分布は、減少、増加、または一定のハザード関数をモデル化して、アイテム寿命の任意のフェーズを示すこともできます。 ## ワイブル曲線はその形状をどう変えるか ワイブル分布は、どれほど柔軟なのでしょうか？[Minitab Statistical Software](https://www.minitab.com/ja-jp/products/minitab/)の \[グラフ\] > \[確率分布プロット\]を使用して、例を見てみましょう（一緒にMinitabを操作してみたいものの、まだ持っていないという方は、[30日間の無料トライアル](https://www.minitab.com/ja-jp/products/minitab/free-trial/)をダウンロードしましょう）。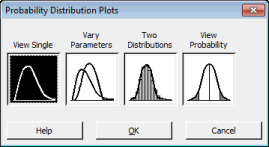  ![probability distribution plots](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/prob_dist_plots_dialog-Jul-05-2025-10-42-05-8953-PM.gif) \[分布\]ドロップダウンメニューで、\[単一表示\]、\[ワイブル\]の順に選択します。ダイアログボックスで、形状、尺度、位置の3つのパラメータを指定できます。 位置パラメータは、分布が0からの移動を示します。負の位置では分布が0の左の方へ移動し、正の位置では分布が0の右の方へ移動します。すべてのデータが位置以上になります。尺度パラメータは、データの63.2百分位点です。平均が正規曲線の場所を定義するように、位置に対するワイブル曲線の関係を定義します。この例では、尺度10を使用します。これは、検定された項目の63.2%が、位置時間の最初の10時間後に故障することを示しています。形状パラメータは、ワイブル曲線の形状を表します。形状を変えながら、異なる寿命分布の特性をモデル化することができます。 この記事では、形状パラメータがワイブル曲線に及ぼす影響だけに焦点を当てます。1つずつ説明しますが、1つのプロットですべてをまとめて表示したい場合は、上のダイアログボックスで\[パラメータ変化\]オプションを選択してください。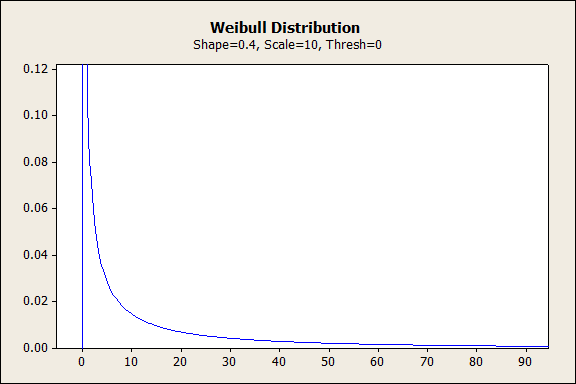  ## 1より小さい形状のワイブル分布 0～1の形状から始めましょう。下の図では、確率が無限から指数関数的に減少しています。故障率の場合、この分布に適合するデータでは初期故障数が多く、時間の経過とともに標本から不良品が排除されるにつれて減少します。この初期故障は製品寿命の初期段階で発生するため、英語では「Infant Mortality」（乳児死亡）と呼ばれたりもします。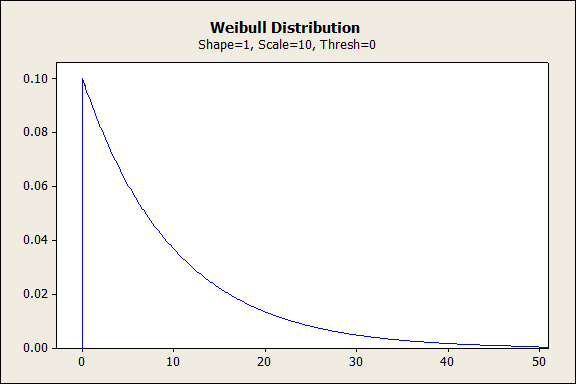   ![Weibull Distribution with shape between 0 and 1](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_1-Jul-05-2025-10-42-10-3202-PM.gif) ## 1に等しい形状のワイブル分布 形状が1に等しい場合、ワイブル分布は1/αから指数関数的に減少します。ここで、αは尺度パラメータです。基本的に、これは時間が経過しても故障率は一定であることを意味します。このワイブル分布の形状は、ランダムな故障や複数原因のある故障に適しており、製品の耐用年数のモデル化に使用できます。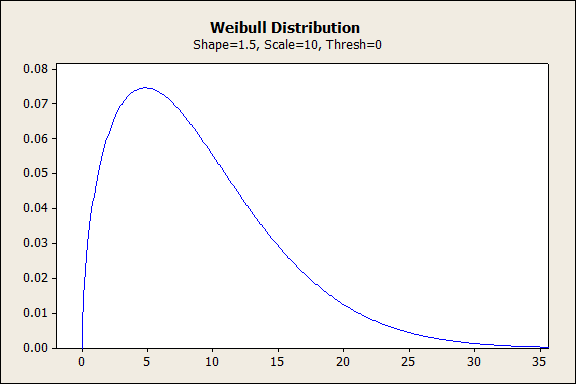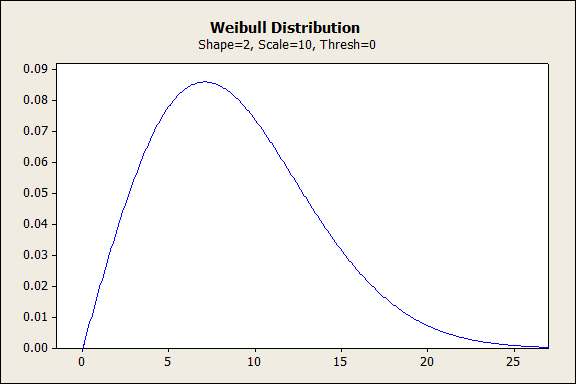  ![Weibull Distribution with shape = 1](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_2-Jul-05-2025-10-42-07-1327-PM.gif) ## 1～2の形状のワイブル分布 形状の値が1～2の場合、ワイブル分布は急速にピークに達し、その後時間の経過とともに減少していきます。故障率は全体的に増加し、最速の増加が初期に発生します。この形状は、初期の摩耗故障を示しています。  ![Weibull Distribution with shape value between 1 and 2](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_3-Jul-05-2025-10-42-03-8584-PM.gif) ## 2に等しい形状のワイブル分布 形状の値が2に達すると、ワイブル分布は直線的に増加する故障率をモデル化します。ここでは、摩耗故障のリスクは製品寿命全体にわたり、一貫して増加します。この形式のワイブル分布は、「レイリー分布」とも呼ばれます。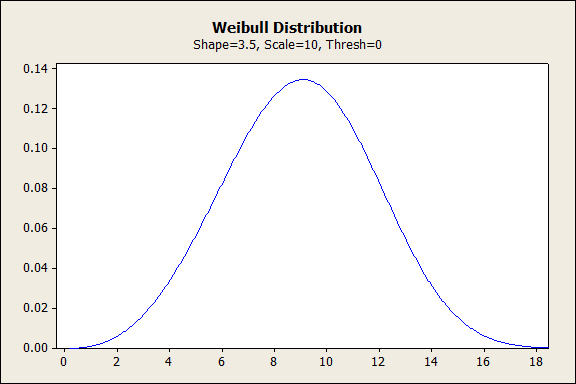  ![Weibull Distribution with Shape = 2 AKA Rayleigh Distribution](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_4-Jul-05-2025-10-42-09-2764-PM.gif)   ## 3～4の形状のワイブル分布 形状の値が3～4の場合、ワイブル分布は正規曲線のように対称な鐘の形になります。この形式のワイブル分布は、製品寿命末期の急速な摩耗故障をモデル化します。この時点でほとんどの故障が発生します。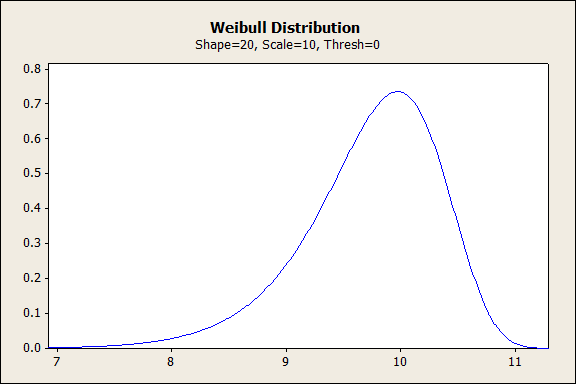 ![Weibull distribution symmetric shape value = 3.5](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_5-Jul-05-2025-10-42-04-9632-PM.gif) ## 10より大きい形状のワイブル分布 形状の値が10より大きい場合、ワイブル分布は極値分布のようになります。この形式の分布も、製品寿命末期をモデル化できます。  ![Weibull Distribution shape value = 20 skewed](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_6-Jul-05-2025-10-42-08-2078-PM.gif) ## ワイブル分布はいつでも最良の選択か？  信頼性となると、ワイブルがよく使われる分布ですが、他の分布族もさまざまな分布形状をモデル化できます。これを覚えておくことは重要です。データに最も適合する分布を見つけたいとき、必ずしもワイブル分布とは限りません。たとえば、化学反応や腐食が原因の製品故障は、通常、対数正規分布でモデル化します。 データの適合を評価するために、Minitabの分布識別プロットを使うことができます（\[統計\] > \[信頼性/生存\] > \[分布分析 (右打ち切りまたは任意打ち切り）\]）。さらなる詳細は、Jim Frostの記事「[データの分布の特定](https://blog.minitab.com/en/adventures-in-statistics-2/how-to-identify-the-distribution-of-your-data-using-minitab?hsLang=ja)」をご覧ください。   ### Signifyでは迅速な市場投入と設計で信頼性獲得：ケーススタディ *ひらめきの瞬間に備えてください！市場投入までの時間と製品の信頼性が競争でものを言う変化の著しい業界で、世界をリードする照明器具会社Signifyが、いかにして革新を迅速に検証するのか、ご覧ください。この1時間のウェビナーでは、W.D. van Driel教授とP. Watté博士が、旧Philips LightingのSignify社で、Minitab Statistical Softwareを使用した信頼性設計に光りを当てます。開発コストを削減し、設計のパフォーマンスとコンプライアンスを高め、製品設計の信頼性の試験を加速させる方法を、実例から学びます。今後数年間、高度な仕様を満たす製品を開発する予定である場合に、製品故障と高くつくクレームのリスクや影響について、貴社および顧客のどちらにとっても抑制となる方法をご覧ください。(英語で提供)* [![ウェビナーを視聴する](https://no-cache.hubspot.com/cta/default/3447555/bdaa2d8b-9365-4806-8e14-4ed2d07547bb.png)](https://cta-redirect.hubspot.com/cta/redirect/3447555/bdaa2d8b-9365-4806-8e14-4ed2d07547bb) [![\[Webinar Replay\] Time-to-Market and Design for Reliability at the Speed of Light at Signify](https://no-cache.hubspot.com/cta/default/3447555/b70a5a3e-03b6-408b-bbc1-7851ef13e4e9.png)](https://cta-redirect.hubspot.com/cta/redirect/3447555/b70a5a3e-03b6-408b-bbc1-7851ef13e4e9) --- - [採用情報](https://www.minitab.com/ja-jp/company/careers/) - [信頼できる窓口](https://www.minitab.com/ja-jp/trust-center/) - [サプライヤー](https://www.minitab.com/ja-jp/suppliers/) - [サイトマップ](https://www.minitab.com/ja-jp/site-map/) - [![linkedin](https://blog.minitab.com/hubfs/WCM/linkedin-1.png)](https://www.linkedin.com/company/minitab/) - [![facebook](https://blog.minitab.com/hubfs/WCM/facebook.png)](https://www.facebook.com/Minitab/) - [![youtube](https://blog.minitab.com/hubfs/WCM/youtube.png)](https://www.youtube.com/user/MinitabInc) - [![instagram](https://blog.minitab.com/hubfs/WCM/instagram.png)](https://www.instagram.com/minitab/) --- © 2025 Minitab, LLC. All Rights Reserved. - [使用条件](https://www.minitab.com/ja-jp/legal/terms-of-use/) - [個人情報保護方針](https://www.minitab.com/ja-jp/legal/privacy-policy/) - [法務](https://www.minitab.com/ja-jp/legal/) - Cookies Settings