--- title: 为什么 Weibull 分布总是广受欢迎 | Why the Weibull Distribution Is Always Welcome description: 涉及可靠性时，Weibull 分布通常是万能分布，但一定要注意的是，其他分布系列也可以对各种分布形状进行建模。 image: https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/welcome_sign-3.jpg --- 中文（简体） - [English](https://blog.minitab.com/en/?hsLang=zh) - [Français](https://blog.minitab.com/fr/?hsLang=zh) - [Deutsch](https://blog.minitab.com/de/?hsLang=zh) - [Português](https://blog.minitab.com/pt/?hsLang=zh) - [Español](https://blog.minitab.com/es/?hsLang=zh) - [日本語](https://blog.minitab.com/ja/?hsLang=zh) - [한국어](https://blog.minitab.com/ko/?hsLang=zh) - [中文（简体）](https://blog.minitab.com/zh/?hsLang=zh) - [Chinese](https://blog.minitab.com/zh/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [Deutsch](https://blog.minitab.com/de/blog/darum-ist-die-weibull-verteilung-überall-willkommen) - [English](https://blog.minitab.com/en/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [Français](https://blog.minitab.com/fr/blog/pourquoi-la-loi-de-weibull-est-elle-souvent-la-plus-utile-explications) - [한국어](https://blog.minitab.com/ko/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [日本語](https://blog.minitab.com/ja/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [![Icon Partners](https://blog.minitab.com/hubfs/WCM/Partners.png) 合作伙伴](https://www.minitab.com/zh-cn/company/partners/) - [![Icon Contact](https://blog.minitab.com/hubfs/WCM/Contact.png) 联系](https://www.minitab.com/zh-cn/company/contact-us/) - [![Icon Talk to Minitab](https://blog.minitab.com/hubfs/WCM/Phone.png) 与 Minitab 沟通](https://www.minitab.com/zh-cn/talk-to-minitab/) - [![Icon My Account](https://blog.minitab.com/hubfs/WCM/MyAcct.png) 我的帐户](https://licensing.minitab.com/account/manage) [![Minitab](https://blog.minitab.com/hubfs/WCM/minitab-corp-logo.svg)](https://www.minitab.com/zh-cn/) - 产品 返回 [产品](https://www.minitab.com/zh-cn/products/) [所有产品](https://www.minitab.com/zh-cn/products/) - [Minitab Solution Center](https://www.minitab.com/zh-cn/products/minitab-solution-center/) - [Minitab Statistical Software](https://www.minitab.com/zh-cn/products/minitab/) - [Minitab Connect](https://www.minitab.com/zh-cn/products/connect/) - [Minitab Model Ops](https://www.minitab.com/zh-cn/products/model-ops/) - [Minitab Education Hub](https://www.minitab.com/zh-cn/products/education-hub/) - [Minitab Engage](https://www.minitab.com/zh-cn/products/engage/) - [Minitab Workspace](https://www.minitab.com/zh-cn/products/workspace/) - [Real-Time SPC](https://www.minitab.com/zh-cn/products/real-time-spc/) - [Prolink 数据收集和统计过程控制 (SPC)](https://info.minitab.com/zh/shop-floor-connectivity-with-prolink?hsLang=zh) - [Simul8 离散事件模拟](https://info.minitab.com/zh/new-to-simul8?hsLang=zh) - [SPM](https://www.minitab.com/zh-cn/products/spm/) - 解决方案 返回 [解决方案](https://www.minitab.com/zh-cn/solutions/) [所有解决方案](https://www.minitab.com/zh-cn/solutions/) - [分析](https://www.minitab.com/zh-cn/solutions/analytics/) - [统计学和预测分析](https://www.minitab.com/zh-cn/solutions/analytics/statistical-analysis-predictive-analytics/) - [数据科学和机器学习](https://www.minitab.com/zh-cn/solutions/analytics/data-science-machine-learning/) - [业务分析和智能软件](https://www.minitab.com/zh-cn/solutions/analytics/business-analytics-intelligence/) - [统计过程控制](https://www.minitab.com/zh-cn/solutions/analytics/statistical-process-control/) - [运营与质量分析](https://www.minitab.com/zh-cn/solutions/analytics/quality-analytics/) - [Live Analytics](https://www.minitab.com/zh-cn/solutions/analytics/live-analytics/) - [可靠性和寿命数据分析](https://www.minitab.com/zh-cn/solutions/analytics/reliability/) - [离散事件模拟](https://info.minitab.com/zh/new-to-simul8?hsLang=zh) - [过程挖掘](https://info.minitab.com/zh/new-to-simul8?hsLang=zh) - [关键功能](https://www.minitab.com/zh-cn/solutions/key-capabilities/) - [持续改进](https://www.minitab.com/zh-cn/solutions/key-capabilities/continuous-improvement/) - [数据集成和数据准备](https://www.minitab.com/zh-cn/solutions/key-capabilities/data-integration-data-prep/) - [图表和思维导图](https://www.minitab.com/zh-cn/solutions/key-capabilities/diagramming-mind-mapping/) - [数字孪生](https://info.minitab.com/zh/new-to-simul8?hsLang=zh) - [模型和机器学习运营](https://www.minitab.com/zh-cn/solutions/key-capabilities/model-deployment-ml-ops/) - [创新和项目管理](https://www.minitab.com/zh-cn/solutions/key-capabilities/innovation-project-management/) - [过程卓越：检测、纠正和预防](https://www.minitab.com/zh-cn/solutions/key-capabilities/process-excellence/) - [自动化数据收集](https://info.minitab.com/zh/shop-floor-connectivity-with-prolink?hsLang=zh) - [行业解决方案](https://www.minitab.com/zh-cn/solutions/industry/) - [学术](https://www.minitab.com/zh-cn/solutions/industry/academic/) - [能源和自然资源](https://www.minitab.com/zh-cn/solutions/industry/energy-resources/) - [政府和公共部门](https://www.minitab.com/zh-cn/solutions/industry/government/) - [医疗保健](https://www.minitab.com/zh-cn/solutions/industry/healthcare/) - [保险](https://www.minitab.com/zh-cn/solutions/industry/insurance/) - [制造和工业](https://www.minitab.com/zh-cn/solutions/industry/manufacturing-industrial/) - [服务](https://www.minitab.com/zh-cn/solutions/industry/service-industries/) - [软件和技术](https://www.minitab.com/zh-cn/solutions/industry/software-technology/) - [建筑](https://www.minitab.com/zh-cn/solutions/industry/construction/) - [按职能/角色](https://www.minitab.com/zh-cn/solutions/role/) - [工程](https://www.minitab.com/zh-cn/solutions/role/engineering/) - [高级商业智能解决方案](https://www.minitab.com/zh-cn/solutions/role/business-analysts/) - [信息技术](https://www.minitab.com/zh-cn/solutions/role/information-technology/) - [供应链](https://www.minitab.com/zh-cn/solutions/role/supply-chain/) - [客户服务解决方案](https://www.minitab.com/zh-cn/solutions/role/customer-service-contact-center/) - [人力资源](https://www.minitab.com/zh-cn/solutions/role/human-resources/) - [营销数据分析](https://www.minitab.com/zh-cn/solutions/role/marketing/) - [研发](https://www.minitab.com/zh-cn/solutions/role/research-and-development/) - 资源和服务 返回 [资源和服务](https://www.minitab.com/zh-cn/resources-services/) [所有资源和服务](https://www.minitab.com/zh-cn/resources-services/) - [资源](https://www.minitab.com/zh-cn/resources-services/resources/) - [解决方案](https://www.minitab.com/zh-cn/resources-services/resources/case-studies/) - [博客](https://www.minitab.com/zh-cn/resources-services/resources/blog/) - [数据集](https://www.minitab.com/zh-cn/resources-services/resources/data-set/) - [活动 & 活动](https://www.minitab.com/zh-cn/resources-services/resources/events/) - [Education Hub](https://www.minitab.com/zh-cn/resources-services/resources/education-hub/) - [服务](https://www.minitab.com/zh-cn/resources-services/services/) - [培训](https://www.minitab.com/zh-cn/resources-services/services/training/) - [部署](https://www.minitab.com/zh-cn/resources-services/services/deployment/) - [统计咨询](https://www.minitab.com/zh-cn/resources-services/services/statistical-consulting/) - [自定进度的学习](https://www.minitab.com/zh-cn/resources-services/services/self-paced-learning/) - [继续教育](https://www.minitab.com/zh-cn/resources-services/services/continuing-education/) - 支持 返回 [支持](https://www.minitab.com/zh-cn/support/) [技术支持](https://www.minitab.com/zh-cn/support/) - [订阅和激活](https://www.minitab.com/zh-cn/support/subscriptions-and-activation/) - [Minitab Quick Start](https://www.minitab.com/zh-cn/support/quick-start/) - [培训](https://www.minitab.com/zh-cn/resources-services/services/training/) - [安装支持](https://www.minitab.com/zh-cn/support/installation/) - [支持视频](https://www.minitab.com/zh-cn/support/videos/) - [软件文档](https://www.minitab.com/zh-cn/support/documents/) - [软件更新](https://www.minitab.com/zh-cn/support/software-updates/) - [产品下载](https://www.minitab.com/zh-cn/support/downloads/) - [支持策略](https://www.minitab.com/zh-cn/support/policy/) - 公司 返回 [公司](https://www.minitab.com/zh-cn/company/) [公司](https://www.minitab.com/zh-cn/company/) - [关于我们](https://www.minitab.com/zh-cn/company/our-company/) - [领导团队](https://www.minitab.com/zh-cn/company/leadership-team/) - [合作伙伴](https://www.minitab.com/zh-cn/company/partners/) - [职业](https://www.minitab.com/zh-cn/company/careers/) - [联系我们](https://www.minitab.com/zh-cn/company/contact-us/) - [新闻](https://www.minitab.com/zh-cn/company/press-releases/) [试用/购买](https://www.minitab.com/zh-cn/try-buy/) - [Minitab Statistical Software](https://blog.minitab.com/zh/blog/tag/minitab-statistical-software) - [注册](https://info.minitab.com/zh/blog/subscribe?hsLang=zh) ![Minitab](https://20853177.fs1.hubspotusercontent-na1.net/hubfs/20853177/minitab-corp-logo.svg?t=1755011311618) ## 通知 您现在将离开 minitab.com。 单击继续以继续： 继续 回去 # 为什么 Weibull 分布总是广受欢迎 | Why the Weibull Distribution Is Always Welcome Minitab Blog Editor | 8/26/2022 主题: [Minitab Statistical Software](https://blog.minitab.com/zh/blog/tag/minitab-statistical-software), [Weibull](https://blog.minitab.com/zh/blog/tag/weibull) - [Share](https://www.linkedin.com/shareArticle?mini=true&url=https://blog.minitab.com/zh/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) - [Share](https://www.facebook.com/sharer.php?u=https://blog.minitab.com/zh/blog/understanding-statistics/why-the-weibull-distribution-is-always-welcome) 在大学里，我有一个朋友，他无论到哪儿都能融入其中。他中午还在跟一群教授共进午餐，下午就在公园里和嬉皮士踢沙包，晚上又会和当地的摩托车骑手在城里秩序最差的酒吧厮混在一起。第二天，他又和体育爱好者一起打橄榄球，然后和游戏伙伴一起去参加通宵的局域网游戏聚会。在平常的周末，他可能会和校园里一小群积极正派的朋克摇滚乐手参加一场面向各个年龄段的演出，或者和一些城里人饮酒作乐，然后和物理社的朋友一起玩一些 D&D 游戏来结束这个周末。  他就像一只变色龙，跟什么人交往就能投其所好，打成一片。这种灵活性让他在各种各样的社交圈中如鱼得水。   他叫 Jeff Weibull，他非常受欢迎，以至于当地统计人员甚至以他的名字命名“Weibull 分布”。   是什么使得 WEIBULL 分布如此受人欢迎？   好吧，我只是编造了最后一部分 — Jeff 的姓实际上并不是“Weibull”，此分布[完全是以其他人的名字](http://en.wikipedia.org/wiki/Waloddi_Weibull)命名的。  但是，当我第一次了解 Weibull 分布时，我立刻想起了 Jeff，以及他似乎不费吹灰之力就能在形形色色的社交场合中游刃有余的场景。   正如 Jeff 是不同社交圈子中的变色龙一样，Weibull 分布能够呈现许多不同类型分布的特征。这使得它在工程师和质量从业者中极受青睐，他们使该分布成为可靠性数据建模中最常用的分布。他们喜欢将 Weibull 分布纳入其数据分析中，因为它足够灵活，可以对各种数据集进行建模。   获得了右偏斜数据？Weibull 可以对其进行建模。左偏斜数据？当然，使用 Weibull 绝对没问题。对称数据？Weibull 能够胜任。正是因为 Weibull 分布的这种灵活性，工程师才用它来评估所有物品（从真空管、电容器到滚珠轴承和继电器等）的可靠性和材料强度。  Weibull 分布还可以对递减、递增或固定风险函数进行建模，使其能够描述物品寿命的任何阶段。  WEIBULL 曲线如何改变其形状  那么，Weibull 分布到底有多灵活呢？让我们来看一些使用 [Minitab Statistical Software](http://www.minitab.com/products/minitab) 中的**图形 > 概率分布图**的示例。（若想继续使用 Minitab 但尚未购买 Minitab，请[下载免费 30 天试用版](https://www.minitab.com/zh-cn/products/minitab/free-trial/)。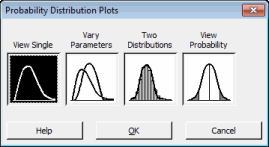）   ![probability distribution plots](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/prob_dist_plots_dialog-Jul-05-2025-10-42-55-7442-PM.gif) 在“分布”下拉菜单中依次选择“单一视图”和“Weibull”。该对话框将用于指定三个参数：形状、尺度和阈值。    阈值参数指示分布从 0 偏移的情况，负阈值会将分布从 0 向左偏移，正阈值会将分布向右偏移。所有数据都必须大于阈值。尺度参数是数据的 63.2 百分位数，它定义了 Weibull 曲线与阈值的关系，就像均值定义正态曲线的位置一样。在我们的示例中，我们使用的尺度为 10，即 63.2% 的测试产品将在阈值时间后的前 10 个小时内发生故障。形状参数描述 Weibull 曲线的形状。通过更改形状，可以对许多不同寿命分布的特征进行建模。  在本帖中，我将专门讨论形状参数如何影响 Weibull 曲线。我将逐一介绍这些参数，但是，如果您希望它们同时出现在一张图中，请在上面显示的对话框中选择“不同参数”选项。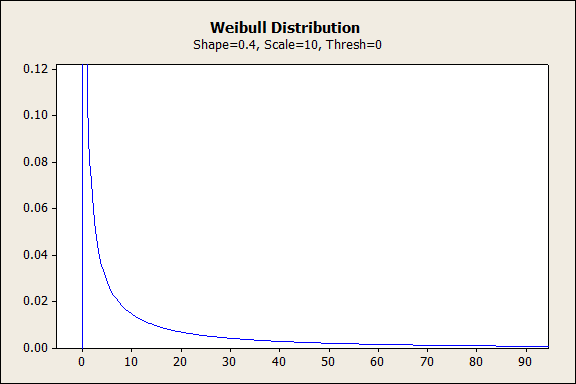   形状值小于 1 的 WEIBULL 分布  让我们从 0 到 1 之间的形状开始。下图显示概率从无穷大呈指数递减的情况。就失效率而言，符合此分布的数据的初始失效率极高，随着时间的推移，由于缺陷产品从样本中消除，因此失效率会下降。这些早期失效通常被称为“早期损坏率”，因为它们发生在产品寿命的早期阶段。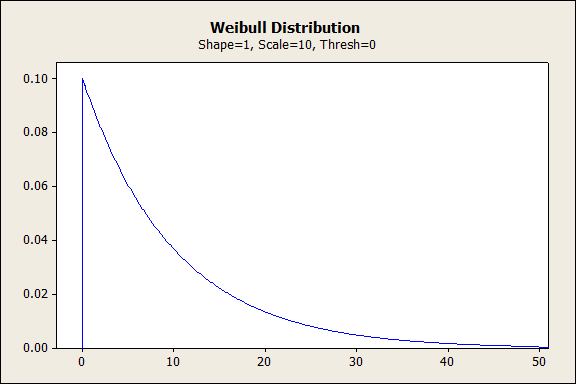    ![Weibull Distribution with shape between 0 and 1](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_1-Jul-05-2025-10-43-00-0080-PM.gif) 形状值等于 1 的 WEIBULL 分布  当形状值等于 1 时，Weibull 分布从 1/alpha 呈指数递减，其中 alpha = 尺度参数。在本质上，这表示失效率随着时间的推移保持一致。Weibull 分布的这种形状适用于随机失效和多原因失效，并可用于对产品的使用寿命进行建模。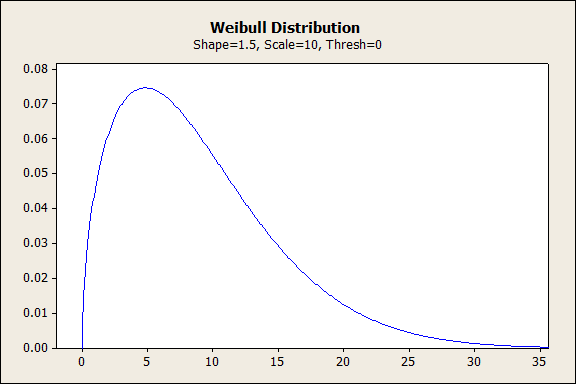   ![Weibull Distribution with shape = 1](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_2-Jul-05-2025-10-42-56-8232-PM.gif) 形状值介于 1 和 2 之间的 WEIBULL 分布  当形状值介于 1 和 2 之间时，Weibull 分布迅速攀升到峰值，然后随着时间的推移下降。失效率总体上是增加的，最初增加得最快。此形状表示早期磨损失效。   ![Weibull Distribution with shape value between 1 and 2](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_3-Jul-05-2025-10-42-52-4992-PM.gif)  形状值等于 2 的 WEIBULL 分布  当形状值达到 2 时，Weibull 分布对线性增加的失效率进行建模，在产品的使用寿命内，磨损失效风险随着时间的推移不断增加。这种形式的 Weibull 分布也称为 Rayleigh 分布。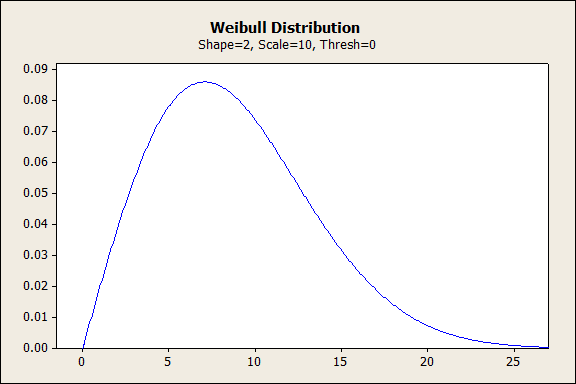   ![Weibull Distribution with Shape = 2 AKA Rayleigh Distribution](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_4-Jul-05-2025-10-42-58-9153-PM.gif)   形状值介于 3 和 4 之间的 WEIBULL 分布  如果我们将形状值放在 3 和 4 之间，Weibull 分布就会变为对称的钟形，就像正态曲线一样。这种形式的 Weibull 分布对产品寿命的最后阶段（大多数失效发生在这一阶段）中的快速磨损失效进行建模。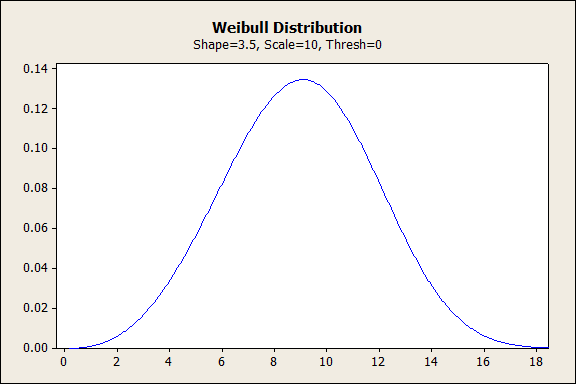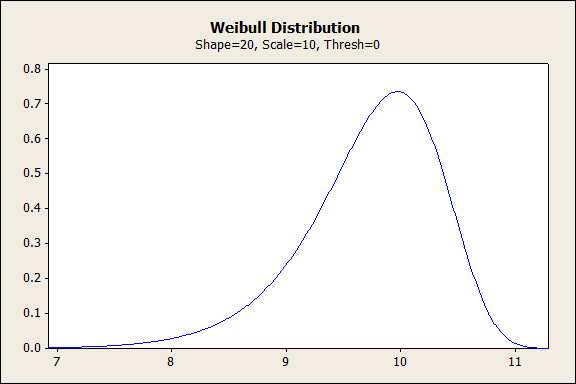  ![Weibull distribution symmetric shape value = 3.5](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_5-Jul-05-2025-10-42-54-6585-PM.gif) 形状值大于 10 的 WEIBULL 分布  当形状值大于 10 时，Weibull 分布类似于极值分布。同样，这种形式的分布可以对产品寿命的最后阶段进行建模。   ![Weibull Distribution shape value = 20 skewed](https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/weibull_distribution_6-Jul-05-2025-10-42-57-8762-PM.gif) ## I WEIBULL 永远是最佳选择吗？   涉及可靠性时，Weibull 分布通常是万能分布，但一定要注意的是，其他分布系列也可以对各种分布形状进行建模。您希望找到最适合您的数据的分布，而这可能不是 Weibull 分布形式。例如，由化学反应或腐蚀引起的产品失效通常采用对数正态分布进行建模。  您可以使用 Minitab 的分布 ID 图来评估数据的拟合情况（统计 > 可靠性/生存 > 分布分析(右删失或任意删失)）。如果您想了解更多详细信息，请查看 Jim Frost 撰写的有关[确定数据分布](https://blog.minitab.com/blog/adventures-in-statistics/how-to-identify-the-distribution-of-your-data-using-minitab?hsLang=zh)的帖子。      [![观看在线研讨会](https://no-cache.hubspot.com/cta/default/3447555/95448e87-69d6-4208-8dcc-95e82c18703d.png)](https://cta-redirect.hubspot.com/cta/redirect/3447555/95448e87-69d6-4208-8dcc-95e82c18703d) [![\[Webinar Replay\] Time-to-Market and Design for Reliability at the Speed of Light at Signify](https://no-cache.hubspot.com/cta/default/3447555/b70a5a3e-03b6-408b-bbc1-7851ef13e4e9.png)](https://cta-redirect.hubspot.com/cta/redirect/3447555/b70a5a3e-03b6-408b-bbc1-7851ef13e4e9) ## 你可能也喜欢 [Minitab Solution Center：搭建数据和决策的桥梁 | The Minitab Solution Center: Bridging Data and Decision-Making](https://blog.minitab.com/zh/blog/the-minitab-solution-center-bridging-data-and-decision-making-1?hsLang=zh) [Minitab Solution Center](https://blog.minitab.com/zh/blog/tag/minitab-solution-center) | 16 分钟阅读 [模拟如何让您保持行业领先——从汽车制造到航空航天](https://blog.minitab.com/zh/blog/how-simulation-keeps-you-ahead-from-automotive-to-aerospace?hsLang=zh) [Minitab Solution Center](https://blog.minitab.com/zh/blog/tag/minitab-solution-center) | 5 分钟阅读 [使用 Minitab 解决方案中心的数据中心简化数据管理 | Streamlined Data Management with the Data Center in the Minitab Solution Center](https://blog.minitab.com/zh/blog/streamlined-data-management-with-the-data-center-in-the-minitab-solution-center?hsLang=zh) [Minitab Solution Center](https://blog.minitab.com/zh/blog/tag/minitab-solution-center) | 5 分钟阅读 --- - [职业](https://www.minitab.com/zh-cn/company/careers/) - [信任中心](https://www.minitab.com/zh-cn/trust-center/) - [供应商](https://www.minitab.com/zh-cn/suppliers/) - [站点图](https://www.minitab.com/zh-cn/site-map/) - [![linkedin](https://blog.minitab.com/hubfs/WCM/linkedin-1.png)](https://www.linkedin.com/company/minitab/) - [![facebook](https://blog.minitab.com/hubfs/WCM/facebook.png)](https://www.facebook.com/Minitab/) - [![youtube](https://blog.minitab.com/hubfs/WCM/youtube.png)](https://www.youtube.com/user/MinitabInc) - [![instagram](https://blog.minitab.com/hubfs/WCM/instagram.png)](https://www.instagram.com/minitab/) --- © 2025 Minitab, LLC. All Rights Reserved. - [使用条款](https://www.minitab.com/zh-cn/legal/terms-of-use/) - [隐私政策](https://www.minitab.com/zh-cn/legal/privacy-policy/) - [合法](https://www.minitab.com/zh-cn/legal/) - Cookies Settings