As Halloween approaches, you are probably taking the necessary steps to protect yourself from the various ghosts, goblins, and witches that are prowling around. Monsters of all sorts are out to get you, unless they’re sufficiently bribed with candy offerings!
I’m here to warn you about a ghoul that all statisticians and data scientists need to be aware of: phantom degrees of freedom. These phantoms are really sneaky. You can be out, fitting a regression model, looking at your output, and thinking everything is fine. Then, whammo, these phantoms get you! They suck the explanatory and predictive power right out of your regression model but, deviously, leave all of the output looking just fine. Now that’s truly spooky!
In this blog post, I’ll show you how these phantoms work and how to avoid their dastardly deeds!
What Are Normal Degrees of Freedom in Regression Models?
I’ve written previously about the dangers of overfitting your regression model. An overfit model is one that is too complicated for your data set.
You can learn only so much from a data set of a given size. A degree of freedom is a measure of how much you’ve learned. Your model uses these degrees of freedom with every parameter that it estimates. If you use too many, you’re overfitting the model. The end result is that the regression coefficients, p-values, and R-squared can all be misleading.
You can detect overfit models by looking at the number of observations per parameter estimate and assessing the predicted R-squared. However, these methods won’t necessarily detect the misbegotten effects of summoning an excessive number of phantom degrees of freedom!
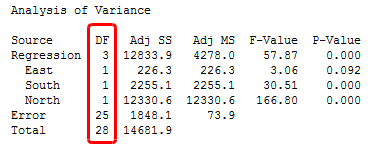
In the degrees of freedom (DF) column in the ANOVA table below, you can see that this regression model uses 3 degrees of freedom out of a total of 28. It appears that this model is fine. Or is it? <Cue evil laugh!>
What Are Phantom Degrees of Freedom?
Phantom degrees of freedom are devilish because they latch onto you through the manner in which you settle on the final model. They are not detectable in the output for the final model even as they haunt your regression models.

The dangers of invoking too many phantom degrees of freedom!
Every time your incantation adds or removes predictors from a model based on a statistical test, you invoke a phantom degree of freedom because you’re learning something from your data set. However, even when you summon many phantom degrees of freedom during the model selection process, they are not evident in Minitab’s output for the final model. That is what makes them phantoms.
When you invoke too many phantoms, your regression model becomes haunted. This occurs because you’re performing many statistical tests, and every statistical test has a false positive rate. When you try many different models, you're bound to find variables that appear to be significant but are correlated only by chance. These relationships are nothing more than ghostly apparitions!
To protect yourself from this type of bewitching, you need to understand the environment that these phantoms inhabit. Phantom degrees of freedom have the strongest powers when you have a small-to-moderate sample size, many potential predictors, correlated predictors, and when the light of knowledge does not illuminate your conception of the true model.
In this scenario, you are likely to fit many possible models, adding and removing different predictors, and testing curvature and interaction terms in an attempt to conjure an answer out of the darkness. Perhaps you use an automatic incantation procedure like stepwise or best subsets regression. If you have multicollinearity, the parameter estimates are particularly unhinged.
The ANOVA table we saw above appears to be perfectly normal, but it could be haunted. To divine the truth, you must understand the entire ritual that incited the final model to materialize. If you start out with 20 variables, a sample size of 29, and fit many models to see what works, you could conjure a possessed model beguiling you to accept false conclusions.
In fact, this method of dredging through data to see what sticks casts such a diabolical spell that it can manifest a statistically significant regression model with a high R-squared from completely random data! Beware—this is the environment that the phantoms inhabit!
How to Protect Yourself from the Phantom Degrees of Freedom
To protect yourself from phantom degrees of freedom, information and advance planning are your best talismans. Use the following rites to shine the light of truth on your research and to guide yourself out of the darkness:
- Conduct prior research about the important variables and their relationships to help you specify the best regression model without the need for data mining.
- Collect a large enough sample size to support the level of model complexity that you will need.
- Avoid data mining and keep track of how many phantom degrees of freedom that you raise before arriving at your final model.
For more information about avoiding haunted models, read my post about How to Choose the Best Regression Model.
Happy Halloween!
"Buer." Licensed under Public Domain via Commons.



