One-way ANOVA can detect differences between the means of three or more groups. It’s such a classic statistical analysis that it’s hard to imagine it changing much.
However, a revolution has been under way for a while now. Fisher's classic one-way ANOVA, which is taught in Stats 101 courses everywhere, may well be obsolete thanks to Welch’s ANOVA.
In this post, I not only want to introduce you to Welch’s ANOVA, but also highlight some interesting research that we perform here at Minitab that guides the implementation of features in our statistical software.
One-Way ANOVA Assumptions
Like any statistical test, one-way ANOVA has several assumptions. However, some of these assumptions are stringent requirements, while others can be waived. Simulation studies can determine which assumptions are true requirements.
For one-way ANOVA, we’ll look at two major assumptions. One of these assumptions is a true requirement, and understanding that explains why Welch’s ANOVA beats the traditional one-way ANOVA.
The discussion below is a summary of simulation studies conducted by Rob Kelly, a senior statistician here at Minitab. You can read the full results in the one-way ANOVA white paper. You can also peruse all of our technical white papers to see the research we conduct to develop methodology throughout the Assistant and Minitab.
Assumption: Samples are drawn from normally distributed populations
One-way ANOVA assumes that the data are normal. However, the simulations show that the test is accurate with nonnormal data when the sample sizes are large enough. These guidelines are:
- If you have 2-9 groups, the sample size for each group should be at least 15.
- If you have 10-12 groups, the sample size for each group should be at least 20.
Assumption: The populations have equal standard deviations (or variances)
One-way ANOVA also assumes that all groups share a common standard deviation even if they have different means. The simulations show that this assumption is stricter than the normality assumption. You can’t waive it away with a large sample size.
What happens if you violate the assumption of equal variances?
For hypothesis tests like ANOVA, you set a significance level. The significance level is the probability that the test incorrectly rejects the null hypothesis (Type I error). This error causes you to incorrectly conclude that the group means are different.
If you set the significance level to the common value of 0.05, 1 out of 20 tests should produce this error.
Rob ran 10,000 simulation runs for each of 50 different conditions to compare the observed error rate to the target level. Ideally, if you set the significance level to 0.05, the observed error rate is also 0.05.
The greater the difference between the target and actual error rate, the more sensitive one-way ANOVA is to violations of the equal variances assumption.
Simulation results for unequal variances
The simulations show that unequal standard deviations cause the actual error rate to diverge from the target rate for the traditional one-way ANOVA.
The best case scenario for unequal standard deviations is when group sizes are equal. With a significance level of 0.05, the observed error rate ranges from 0.02 to 0.08.
For unequal group sizes, the results varied greatly depending on the standard deviations of the larger and smaller groups. The error rates for unequal group sizes extend up to 0.22!
Solutions to this Problem
Clearly you need to be wary when you perform one-way ANOVA and your group standard deviations are potentially different. Fortunately, there are two approaches you can try.
Test for equal variances
In Minitab, you can perform a test to determine whether the standard deviations of the groups are significantly different: Stat > ANOVA > Test for Equal Variances. If the test’s p-value is greater than 0.05, there is insufficient evidence to conclude that the standard deviations are different.
However, there is a big caveat. Even if you meet the sample size guidelines for one-way ANOVA, the test for equal variances may have insufficient power. In this case, your groups can have unequal standard deviations but the test will be unlikely to detect the difference. In general, failing to reject the null hypothesis is not the best method to determine that groups are equal.
However, if you have an adequate sample size and if the variance test’s p-value is greater than 0.05, you can trust the results from the traditional one-way ANOVA.
Welch’s ANOVA
What do you do if the test for equal variances indicates that the standard deviations are different? Or that the test has insufficient power? Or, perhaps you just don’t want to have to worry about performing and explaining this extra test? Let me introduce you to Welch’s ANOVA!
Welch’s ANOVA is an elegant solution because it is a form of one-way ANOVA that does not assume equal variances. And the simulations show that it works great!
When the group standard deviations are unequal and the significance level is set at 0.05, the simulation error rate for:
- The traditional one-way ANOVA ranges from 0.02 to 0.22, while
- Welch’s ANOVA has a much smaller range, from 0.046 to 0.054.
Additionally, for cases where the group standard deviations are equal, there is only a negligible difference in statistical power between these two procedures.
Where to Find Welch’s ANOVA in Minitab
You might be using Welch’s ANOVA already without realizing it. Because of the advantages described above, the Assistant only performs Welch’s ANOVA.
You can also perform Welch’s ANOVA outside of the Assistant. Go to Stat > ANOVA > One-Way. Click Options, and uncheck Assume equal variances. You can also perform multiple comparisons using the Games-Howell method to identify differences between pairs of groups.
Below is example output for Welch's ANOVA from the Assistant. Just like the classic one-way ANOVA, look at the p-value to determine significance and use the Means Comparison Chart to look for differences between specific groups.
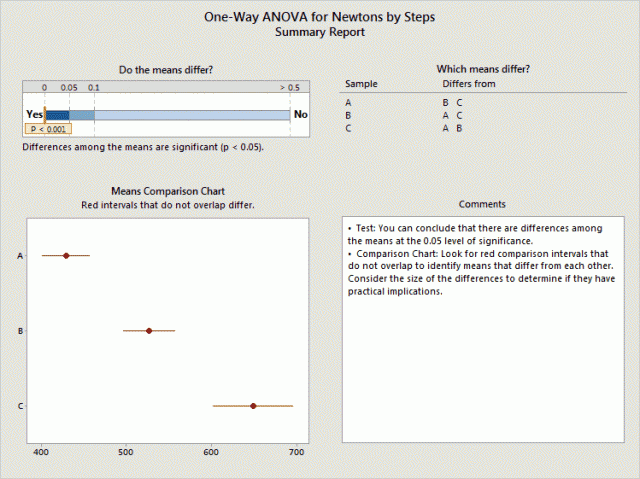
The low p-value (< 0.001) indicates that at least one mean is different. The chart shows that each mean is different from the other two means.



