In my previous post, I highlighted recent academic research that shows how the presentation style of regression results affects the number of interpretation mistakes. In this post, I present four tips that will help you avoid the more common mistakes of applied regression analysis that I identified in the research literature.
I’ll focus on applied regression analysis, which is used to make decisions rather than just determining the statistical significance of the predictors. Applied regression analysis emphasizes both being able to influence the outcome and the precision of the predictions.
Tip 1: Use Prior Studies to Determine which Variables to Include in the Regression Model
Before beginning the regression analysis, you should already have an idea of what the important variables are along with their relationships, coefficient signs, and effect magnitudes based on previous research. Unfortunately, recent trends have moved away from this approach thanks to large, readily available databases and automated procedures that build regression models.
If you want see the problem with data mining in action, simply create a worksheet in Minitab Statistical Software that has 101 columns, each of which contains 30 rows of random data, or use this worksheet. Then, perform stepwise regression using one column as the response variable and all of the others as the potential predictor variables. This simulates dredging through a data set to see what sticks.
The results below are for the entirely random data. Each column in the output shows the model fit statistics for the first 5 steps of the stepwise procedure. For five predictors, we got an R-squared of 84.23% and an adjusted R-squared of 80.12%! The p-values (not shown) are all very low, often less than 0.01!
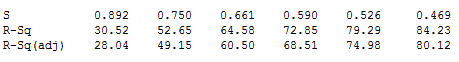
While stepwise regression and best subsets regression have their place in the early stages, you need more reason to include a predictor variable in a final regression model than just being able to reject the null hypothesis.
Tip 2: Keep the Model Simple
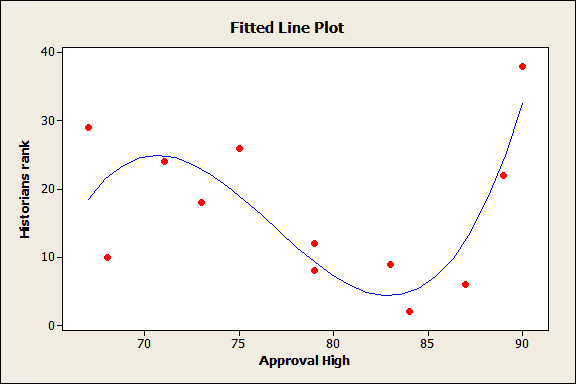 This model is too complex. Read why here.
This model is too complex. Read why here.
While it may seem reasonable that complex problems require complex models, many studies show that simpler models generally produce more precise predictions. How simple? In many cases, three predictor variables are sufficient.
Start simple, and only make the model more complex as needed. Be sure to confirm that the added complexity truly improves the precision. While complexity tends to increase the model fit (r-squared), it also tends to lower the precision of the predictions (wider prediction intervals).
I write more about this tradeoff and how to include the correct number of variables in my post about adjusted and predicted r-squared.
Tip 3: Correlation is Not Causation . . . Even in Regression Analysis
This statistical truth seems simple enough. However, in regression analysis, people often forget this rule. You can have a well-specified model with significant predictors, a high r-squared, and yet you might only be uncovering correlation rather than causation!
Regression analysis outside of an experimental design is not a good way to identify causal relationships between variables.
In some cases, this is just fine. Prediction doesn’t always require a causal relationship between predictor and response. Instead, a proxy variable that is simply correlated to the response, and is easier to obtain than a causally connected variable, might produce adequate predictions.
However, if you want to affect the outcome by setting predictor values, you need to identify the truly causal relationships.
To illustrate this point, it has been hard for studies that don’t use randomized controlled trials to determine whether vitamins improve health, or if vitamin consumption is simply correlated to healthy habits that actually improve health (read my post). Put simply, if vitamin consumption doesn’t cause good health, then consuming more vitamins won’t improve your health.
Tip 4: Present Confidence and Prediction Intervals in Addition to Statistical Significance
Confidence intervals and statistical significance provide consistent information. For example, if a statistic is significantly different from zero at the 0.05 alpha level, you can be sure that the 95% confidence interval does not contain zero.
While the information is consistent, it changes how people use the information. This issue is similar to that raised in my previous post, where presentation style affects interpretation accuracy. A study by Cumming found that reporting significance levels produced correct conclusions only 40% of the time, while including confidence intervals yielded correct interpretations 95% of the time.
For more on this, read my post where I examine when you should use confidence intervals, prediction intervals, and tolerance intervals.
How Do You Distinguish a Good Regression Analysis from a Less Rigorous Regression Analysis?
For a good regression analysis, the analyst:
- Uses large amounts of trustworthy data and a small number of predictors that have well established causal relationships.
- Uses sound reasoning for including variables in the model.
- Brings together different lines of research as needed.
- Effectively presents the results using graphs, confidence intervals, and prediction intervals in a clear manner that ensures proper interpretation by others.
Conversely, in a less rigorous regression analysis, the analyst:
- Uses regression outside of an experiment to search for causal relationships.
- Falls into the trap of data-mining because databases provide a lot of convenient data.
- Includes a variable in the model simply because he can reject the null hypothesis.
- Uses a complex model to increase the r-squared value.
- Reports only the standard statistics of coefficients, p-values, and r-squared values, even though this approach tends to produce inaccurate interpretations even among experts.
If you're learning about regression, read my regression tutorial!
________________________________
Armstrong J., Illusions in Regression Analysis, International Journal of Forecasting, 2012 (3), 689-694.
Cumming, G. (2012), Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta Analysis. New York: Routledge.
Ord, K. (2012), The Illusion of Predictability: A call to action, International Journal of Forecasting, March 5, 2012.
Zellner, A. (2001), Keep it sophisticatedly simple. In Keuzenkamp, H. & McAleer, M. Eds. Simplicity, Inference, and Modelling: Keeping it Sophisticatedly Simple. Cambridge University Press, Cambridge.



