---
title: What Is the F-test of Overall Significance in Regression Analysis?
description: What Is the F-test of Overall Significance in Regression Analysis?
image: https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/ftest_anova_table-Jul-06-2025-12-12-30-9407-AM.png
---
English
- [English](https://blog.minitab.com/en/?hsLang=en)
- [Français](https://blog.minitab.com/fr/?hsLang=en)
- [Deutsch](https://blog.minitab.com/de/?hsLang=en)
- [Português](https://blog.minitab.com/pt/?hsLang=en)
- [Español](https://blog.minitab.com/es/?hsLang=en)
- [日本語](https://blog.minitab.com/ja/?hsLang=en)
- [한국어](https://blog.minitab.com/ko/?hsLang=en)
- [中文（简体）](https://blog.minitab.com/zh/?hsLang=en)
- [English](https://blog.minitab.com/en/blog/adventures-in-statistics-2/what-is-the-f-test-of-overall-significance-in-regression-analysis)
- [Português](https://blog.minitab.com/pt/blog/o-que-o-teste-f-de-significancia-global-na-analise-de-regressao)
- [한국어](https://blog.minitab.com/ko/blog/adventures-in-statistics-2/what-is-the-f-test-of-overall-significance-in-regression-analysis)
- [ Partners](https://www.minitab.com/en-us/company/partners/)
- [ Contact](https://www.minitab.com/en-us/company/contact-us/)
- [ Talk to Minitab](https://www.minitab.com/en-us/talk-to-minitab/)
- [ My Account](https://licensing.minitab.com/account/manage)
[](https://www.minitab.com/en-us/)
- Products
Back
[Products](https://www.minitab.com/en-us/products/)
[All Products](https://www.minitab.com/en-us/products/)
- [Minitab Solution Center](https://www.minitab.com/en-us/products/minitab-solution-center/)
- [Minitab Statistical Software](https://www.minitab.com/en-us/products/minitab/)
- [Minitab Connect](https://www.minitab.com/en-us/products/connect/)
- [Minitab Model Ops](https://www.minitab.com/en-us/products/model-ops/)
- [Minitab Education Hub](https://www.minitab.com/en-us/products/education-hub/)
- [Minitab Engage](https://www.minitab.com/en-us/products/engage/)
- [Minitab Workspace](https://www.minitab.com/en-us/products/workspace/)
- [Real-Time SPC](https://www.minitab.com/en-us/products/real-time-spc/)
- [Prolink Data Collection & SPC](https://www.minitab.com/en-us/products/prolink)
- [Simul8 Discrete Event Simulation](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [SPM](https://www.minitab.com/en-us/products/spm/)
- Solutions
Back
[Solutions](https://www.minitab.com/en-us/solutions/)
[All Solutions](https://www.minitab.com/en-us/solutions/)
- [Analytics](https://www.minitab.com/en-us/solutions/analytics/)
- [Statistics & Predictive Analytics](https://www.minitab.com/en-us/solutions/analytics/statistical-analysis-predictive-analytics/)
- [Data Science & Machine Learning](https://www.minitab.com/en-us/solutions/analytics/data-science-machine-learning/)
- [Business Analytics & Intelligence](https://www.minitab.com/en-us/solutions/analytics/business-analytics-intelligence/)
- [Statistical Process Control](https://www.minitab.com/en-us/solutions/analytics/statistical-process-control/)
- [Quality Analytics](https://www.minitab.com/en-us/solutions/analytics/quality-analytics/)
- [Live Analytics](https://www.minitab.com/en-us/solutions/analytics/live-analytics/)
- [Reliability & Life Data Analysis](https://www.minitab.com/en-us/solutions/analytics/reliability/)
- [Discrete Event Simulation](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [Process Mining](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [Key Capabilities](https://www.minitab.com/en-us/solutions/key-capabilities/)
- [Continuous Improvement](https://www.minitab.com/en-us/solutions/key-capabilities/continuous-improvement/)
- [Data Integration & Data Prep](https://www.minitab.com/en-us/solutions/key-capabilities/data-integration-data-prep/)
- [Diagramming & Mind Mapping](https://www.minitab.com/en-us/solutions/key-capabilities/diagramming-mind-mapping/)
- [Digital Twins](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [Model Deployment & ML Ops](https://www.minitab.com/en-us/solutions/key-capabilities/model-deployment-ml-ops/)
- [Innovation & Project Management](https://www.minitab.com/en-us/solutions/key-capabilities/innovation-project-management/)
- [Process Excellence: Detect, Correct & Prevent](https://www.minitab.com/en-us/solutions/key-capabilities/process-excellence/)
- [Featured Industries](https://www.minitab.com/en-us/solutions/industry/)
- [Academic](https://www.minitab.com/en-us/solutions/industry/academic/)
- [Energy & Natural Resources](https://www.minitab.com/en-us/solutions/industry/energy-resources/)
- [Government & Public Sector](https://www.minitab.com/en-us/solutions/industry/government/)
- [Healthcare](https://www.minitab.com/en-us/solutions/industry/healthcare/)
- [Insurance](https://www.minitab.com/en-us/solutions/industry/insurance/)
- [Manufacturing & Industrial](https://www.minitab.com/en-us/solutions/industry/manufacturing-industrial/)
- [Services](https://www.minitab.com/en-us/solutions/industry/service-industries/)
- [Software & Technology](https://www.minitab.com/en-us/solutions/industry/software-technology/)
- [Construction](https://www.minitab.com/en-us/solutions/industry/construction/)
- [Featured Roles](https://www.minitab.com/en-us/solutions/role/)
- [Engineering](https://www.minitab.com/en-us/solutions/role/engineering/)
- [Business Analysis](https://www.minitab.com/en-us/solutions/role/business-analysts/)
- [Information Technology](https://www.minitab.com/en-us/solutions/role/information-technology/)
- [Supply Chain](https://www.minitab.com/en-us/solutions/role/supply-chain/)
- [Customer Service & Contact Center](https://www.minitab.com/en-us/solutions/role/customer-service-contact-center/)
- [Human Resources](https://www.minitab.com/en-us/solutions/role/human-resources/)
- [Marketing](https://www.minitab.com/en-us/solutions/role/marketing/)
- [Research and Development](https://www.minitab.com/en-us/solutions/role/research-and-development/)
- Resources & Services
Back
[Resources & Services](https://www.minitab.com/en-us/resources-services/)
[All Resources & Services](https://www.minitab.com/en-us/resources-services/)
- [Resources](https://www.minitab.com/en-us/resources-services/resources/)
- [Case Studies](https://www.minitab.com/en-us/resources-services/resources/case-studies/)
- [eBooks & White Papers](https://www.minitab.com/en-us/resources-services/resources/ebooks-and-white-papers/)
- [Blog](https://blog.minitab.com/blog/?hsLang=en)
- [Data Sets](https://www.minitab.com/en-us/resources-services/resources/data-set/)
- [Webinars & Events](https://www.minitab.com/en-us/resources-services/resources/events/)
- [Education Hub](https://www.minitab.com/en-us/resources-services/resources/education-hub/)
- [Services](https://www.minitab.com/en-us/resources-services/services/)
- [Training](https://www.minitab.com/en-us/resources-services/services/training/)
- [Deployment](https://www.minitab.com/en-us/resources-services/services/deployment/)
- [Consulting](https://www.minitab.com/en-us/resources-services/services/statistical-consulting/)
- [Self-Paced Learning](https://www.minitab.com/en-us/resources-services/services/self-paced-learning/)
- [Continuing Education](https://www.minitab.com/en-us/resources-services/services/continuing-education/)
- Support
Back
[Support](https://www.minitab.com/en-us/support/)
[Technical Support](https://www.minitab.com/en-us/support/)
- [Subscriptions & Activation](https://www.minitab.com/en-us/support/subscriptions-and-activation/)
- [Minitab Quick Start](https://www.minitab.com/en-us/support/quick-start/)
- [Training](https://www.minitab.com/en-us/resources-services/services/training/)
- [Installation Support](https://www.minitab.com/en-us/support/installation/)
- [Support Videos](https://www.minitab.com/en-us/support/videos/)
- [Support Documentation](https://www.minitab.com/en-us/support/documents/)
- [Software Updates](https://www.minitab.com/en-us/support/software-updates/)
- [Product Downloads](https://www.minitab.com/en-us/support/downloads/)
- [Support Policy](https://www.minitab.com/en-us/support/policy/)
- Company
Back
[Company](https://www.minitab.com/en-us/company/)
[Company](https://www.minitab.com/en-us/company/)
- [About Us](https://www.minitab.com/en-us/company/our-company/)
- [Leadership Team](https://www.minitab.com/en-us/company/leadership-team/)
- [Partners](https://www.minitab.com/en-us/company/partners/)
- [Careers](https://www.minitab.com/en-us/company/careers/)
- [Contact](https://www.minitab.com/en-us/company/contact-us/)
- [News](https://www.minitab.com/en-us/company/press-releases/)
[Try/Buy](https://www.minitab.com/en-us/try-buy/)
- [Statistics](https://blog.minitab.com/en/blog/tag/statistics)
- [Data Analysis](https://blog.minitab.com/en/blog/tag/data-analysis)
-
- [Quality Improvement](https://blog.minitab.com/en/blog/tag/quality-improvement)
- [Subscribe](https://info.minitab.com/blog/subscribe?hsLang=en)
## Notice
You are now leaving minitab.com.
Click Continue to proceed to:
Continue
Go Back
# What Is the F-test of Overall Significance in Regression Analysis?
Minitab Blog Editor | 6/11/2015
Topics: [Regression Analysis](https://blog.minitab.com/en/blog/tag/regression-analysis)
- [Share](https://www.linkedin.com/shareArticle?mini=true&url=https://blog.minitab.com/en/blog/adventures-in-statistics-2/what-is-the-f-test-of-overall-significance-in-regression-analysis)
- [Share](https://www.facebook.com/sharer.php?u=https://blog.minitab.com/en/blog/adventures-in-statistics-2/what-is-the-f-test-of-overall-significance-in-regression-analysis)
Previously, I’ve written about [how to interpret regression coefficients and their individual P values](https://blog.minitab.com/blog/adventures-in-statistics/how-to-interpret-regression-analysis-results-p-values-and-coefficients?hsLang=en).
I’ve also written about [how to interpret R-squared](https://blog.minitab.com/blog/adventures-in-statistics/regression-analysis-how-do-i-interpret-r-squared-and-assess-the-goodness-of-fit?hsLang=en) to assess the strength of the relationship between your model and the response variable.
Recently I've been asked, how does the F-test of the overall significance and its P value fit in with these other statistics? That’s the topic of this post!
In general, an F-test in regression compares the fits of different linear models. Unlike t-tests that can assess only one regression coefficient at a time, the F-test can assess multiple coefficients simultaneously.
The F-test of the overall significance is a specific form of the F-test. It compares a model with no predictors to the model that you specify. A regression model that contains no predictors is also known as an intercept-only model.
The hypotheses for the F-test of the overall significance are as follows:
- **Null hypothesis**: The fit of the intercept-only model and your model are equal.
- **Alternative hypothesis**: The fit of the intercept-only model is significantly reduced compared to your model.
In [Minitab statistical software](http://www.minitab.com/products/minitab/), you'll find the F-test for overall significance in the Analysis of Variance table.
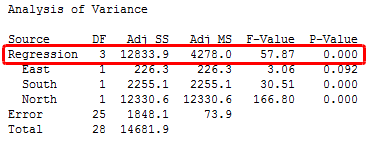
If the P value for the F-test of overall significance test is less than your significance level, you can reject the null-hypothesis and conclude that your model provides a better fit than the intercept-only model.
Great! That set of terms you included in your model improved the fit!
Typically, if you don't have any significant P values for the individual coefficients in your model, the overall F-test won't be significant either. However, in a few cases, the tests could yield different results. For example, a significant overall F-test could determine that the coefficients are *jointly* not all equal to zero while the tests for individual coefficients could determine that all of them are *individually* equal to zero.
There are a couple of additional conclusions you can draw from a significant overall F-test.
In the intercept-only model, all of the fitted values equal the mean of the response variable. Therefore, if the P value of the overall F-test is significant, your regression model predicts the response variable better than the mean of the response.
While R-squared provides an estimate of the strength of the relationship between your model and the response variable, it does not provide a formal hypothesis test for this relationship. The overall F-test determines whether this relationship is statistically significant. If the P value for the overall F-test is less than your significance level, you can conclude that the R-squared value is significantly different from zero.
To see how the F-test works using concepts and graphs, see my post about [understanding the F-test](https://blog.minitab.com/blog/adventures-in-statistics/understanding-analysis-of-variance-anova-and-the-f-test?hsLang=en).
If your entire model is statistically significant, that's great news! However, be sure to [check the residual plots](https://blog.minitab.com/blog/adventures-in-statistics/why-you-need-to-check-your-residual-plots-for-regression-analysis?hsLang=en) so you can trust the results!
If you're learning about regression, read my [regression tutorial](https://blog.minitab.com/blog/adventures-in-statistics/regression-analysis-tutorial-and-examples?hsLang=en)!
## You Might Also Like
[How One Hotel Used Data to Improve Guest Satisfaction](https://blog.minitab.com/en/blog/how-one-hotel-used-data-to-improve-guest-satisfaction?hsLang=en)
[Brainstorm](https://blog.minitab.com/en/blog/tag/brainstorm) | 9 Minute Read
[Enhancing Accelerated Underwriting Efficiency with Predictive Analytics](https://blog.minitab.com/en/blog/enhancing-accelerated-underwriting-efficiency-with-predictive-analytics?hsLang=en)
[Regression Analysis](https://blog.minitab.com/en/blog/tag/regression-analysis) | 3 Minute Read
[Predictive Analytics and Determining Patient Length of Stay at Time of Admission](https://blog.minitab.com/en/blog/predictive-analytics-and-determining-patient-length-of-stay-at-time-of-admission?hsLang=en)
[Regression Analysis](https://blog.minitab.com/en/blog/tag/regression-analysis) | 5 Minute Read
---
- [Careers](https://www.minitab.com/en-us/company/careers/)
- [Trust Center](https://www.minitab.com/en-us/trust-center/)
- [Suppliers](https://www.minitab.com/en-us/suppliers/)
- [Site Map](https://www.minitab.com/en-us/site-map/)
- [](https://www.linkedin.com/company/minitab/)
- [](https://www.facebook.com/Minitab/)
- [](https://www.youtube.com/user/MinitabInc)
- [](https://www.instagram.com/minitab/)
---
© 2025 Minitab, LLC. All Rights Reserved.
- [Terms of Use](https://www.minitab.com/en-us/legal/terms-of-use/)
- [Privacy Policy](https://www.minitab.com/en-us/legal/privacy-policy/)
- [Legal](https://www.minitab.com/en-us/legal/)
- Cookies Settings