In statistics, we use a variety of intervals to characterize the results. The most well-known of these are confidence intervals. However, confidence intervals are not always appropriate. In this post, we’ll take a look at the different types of intervals that are available in Minitab, their characteristics, and when you should use them.
I’ll cover confidence intervals, prediction intervals, and tolerance intervals. Because tolerance intervals are the least-known, I’ll devote extra time to explaining how they work and when you’d want to use them.
What are Confidence Intervals?
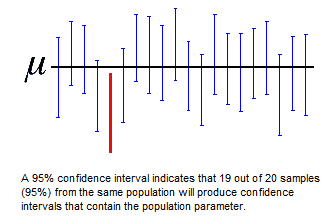A confidence interval is a range of values, derived from sample statistics, that is likely to contain the value of an unknown population parameter. Because of their random nature, it is unlikely that two samples from a given population will yield identical confidence intervals. But if you repeated your sample many times, a certain percentage of the resulting confidence intervals would contain the unknown population parameter. The percentage of these confidence intervals that contain the parameter is the confidence level of the interval.
Most frequently, you’ll use confidence intervals to bound the mean or standard deviation, but you can also obtain them for regression coefficients, proportions, rates of occurrence (Poisson), and for the differences between populations.
Suppose that you randomly sample light bulbs and measure the burn time. Minitab calculates that the 95% confidence interval is 1230 – 1265 hours. The confidence interval indicates that you can be 95% confident that the mean for the entire population of light bulbs falls within this range.
Confidence intervals only assess sampling error in relation to the parameter of interest. (Sampling error is simply the error inherent when trying to estimate the characteristic of an entire population from a sample.) Consequently, you should be aware of these important considerations:
- As you increase the sample size, the sampling error decreases and the intervals become narrower. If you could increase the sample size to equal the population, there would be no sampling error. In this case, the confidence interval would have a width of zero and be equal to the true population parameter.
- Confidence intervals only tell you about the parameter of interest and nothing about the distribution of individual values.
In the light bulb example, we know that the mean is likely to fall within the range, but the 95% confidence interval does not predict that 95% of future observations will fall within the range. We’ll need to use a different type of interval to draw a conclusion like that.
For more information about confidence intervals, please read my blog post: Understanding Hypothesis Tests: Confidence Intervals and Confidence Levels.
What Are Prediction Intervals?
A prediction interval is a type of confidence interval that you can use with predictions from linear and nonlinear models. There are two types of prediction intervals that use predictor values entered into the model equation.
Confidence interval of the prediction
A confidence interval of the prediction is a range that is likely to contain the mean response given specified settings of the predictors in your model. Just like the regular confidence intervals, the confidence interval of the prediction presents a range for the mean rather than the distribution of individual data points.
Going back to our light bulb example, suppose we design an experiment to test how different production methods (Slow or Quick) and filament materials (A or B) affect the burn time. After we fit a model, statistical software like Minitab can predict the response for specific settings. We want to predict the mean burn time for bulbs that are produced with the Quick method and filament type A.
Minitab calculates a confidence interval of the prediction of 1400 – 1450 hours. We can be 95% confident that this range includes the mean burn time for light bulbs manufactured using these settings. However, it doesn’t tell us anything about the distribution of burn times for individual bulbs.
Prediction interval
A prediction interval is a range that is likely to contain the response value of a single new observation given specified settings of the predictors in your model.
We’ll use the same settings as above, and Minitab calculates a prediction interval of 1350 – 1500 hours. We can be 95% confident that this range includes the burn time of the next light bulb produced with these settings.
The prediction interval is always wider than the corresponding confidence interval of the prediction because of the added uncertainty involved in predicting a single response versus the mean response.
We’re getting down to determining where an individual observation is likely to fall, but you need a model for it to work.
What Are Tolerance Intervals?
A tolerance interval is a range that is likely to contain a specified proportion of the population. To generate tolerance intervals, you must specify both the proportion of the population and a confidence level. The confidence level is the likelihood that the interval actually covers the proportion. Let’s look at an example, because that’s the easiest way to understand tolerance intervals.
Example of a tolerance interval
The light bulb manufacturer is interested in how long their light bulbs burn. The analysts randomly sample 100 bulbs and record the burn time in this worksheet.
In Minitab, go to Stat > Quality Tools > Tolerance Intervals. Under Data, choose Samples in columns. In the textbox, enter Hours. Click OK. (If you're not already using it, please download the free 30-day trial of Minitab and play along!)
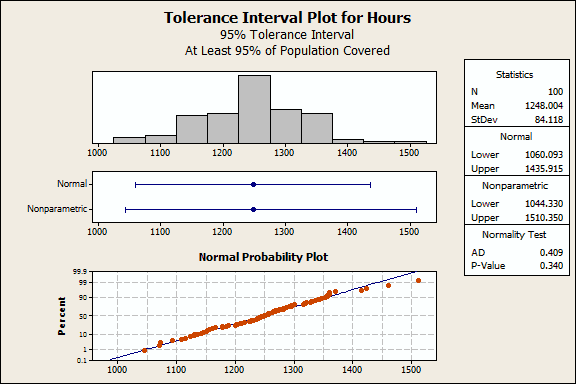
The normality test indicates that our data are normally distributed. Consequently, we can use the Normal interval (1060 1435). The manufacturer is 95% confident that at least 95% of all burn times will fall between 1060 to 1435 hours. If this range is wider than their clients' requirements, the process may produce excessive defects.
How tolerance intervals work compared to confidence intervals
A confidence interval's width is due entirely to sampling error. As the sample size approaches the entire population, the width of the confidence interval approaches zero.
In contrast, the width of a tolerance interval is due to both sampling error and variance in the population. As the sample size approaches the entire population, the sampling error diminishes and the estimated percentiles approach the true population percentiles.
To determine where 95% of the population falls, Minitab calculates the data values that correspond to the estimated 2.5th and 97.5th percentiles (97.5 - 2.5 = 95). Read here for more information about percentiles and population proportions.
Unfortunately, the percentile estimates will have error because we are working with a sample. We can’t be 100% confident that a tolerance interval truly contains the specified proportion. Consequently, tolerance intervals have a confidence level.
Uses for tolerance intervals
In general, use tolerance intervals if you have sampled data and want to predict a range of likely outcomes.
In the quality improvement field, Six Sigma analysts generally require that the output from a process have measurements (e.g., burn time, length, etc.) that fall within the specification limits. In this context, tolerance intervals can detect excessive variation by comparing client requirements to tolerance limits that cover a specified proportion of the population. If the tolerance interval is wider than the client's requirements, there may be too much product variation.
With Minitab Statistical Software, it’s easy to obtain all of these intervals for your data! You just need to be aware of what information each interval provides.