Screening experimental designs allow you to study a very large number of factors in a very limited number of runs. The objective is to focus on the few factors that have a real effect and eliminate the effects that are not significant. This is often the initial typical objective of any experimenter when a DOE (design of experiments) is performed.
Table of Factorial Designs
Consider the table below. In Minitab, you can quickly access this table of factorial designs by selecting Stat > DOE > Factorial > Create Factorial Design... and clicking "Display Available Designs." The table tells us the number of runs in a 2k standard factorial design, its resolution, and the number of factors to be analyzed. If you need to study 8 factors, or 7 factors, or even 6 factors, a 16-run design could be a good choice, because it balances the number of runs with the ability to effectively interpret the experimental results.
Confounding is the price we pay for reducing the number of runs: the effects of different factors or interactions of factors can't be evaluated individually, so interpreting the results becomes more difficult and riskier. The yellow color indicates that this design is acceptable in terms of confounding/resolution. Designs with the green color have limited or no confounding, but a larger number of runs. On the other hand, any experimenter should refrain from using designs located in the red region due to extensive confounding. Red means that some main factors are confounded with two-factor interactions.
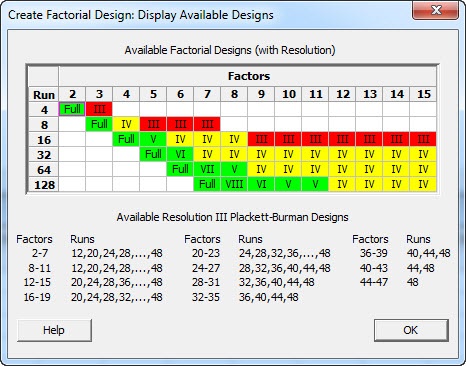
According to the table, studying more than 8 factors means you'll need to perform 32 in order to remain in the yellow region. But when experiments are costly and time consuming, that may be too many.
Plackett-Burman Designs: An Alternative to Factorial
Fortunately, another solution is available: Plackett-Burman designs may be used to analyze a larger number of variables more economically. For example, to study 9 factors you need only conduct 12 runs, rather than the 32 runs needed in a standard 2k fractional design. In the Minitab Assistant, for example, Plackett-Burman designs are suggested whenever the number of factors to be studied is larger than five.
The main disadvantage of this type of screening design is that two-factor interactions cannot be studied. In Plackett-Burman designs, interactions are partially confounded or "aliased" with all main effects. Sometimes the interactions appear with a positive sign, meaning they are summed up to the main effect. In other cases they have a negative sign, indicating they are subtracted from the main effect. One third of each interaction is added to or subtracted from any main effect. For example, in the experimental aliasing table below, the effect of the A factor is partially confounded with all interaction effects:
Alias / confounding structure in a Plackett-Burman design - Aliases :
A - 0.33 BC - 0.33 BD - 0.33 BE + 0.33 BF - 0.33 BG - 0.33 BH + 0.33 CD - 0.33 CE - 0.33 CF + 0.33 CG - 0.33 CH + 0.33 DE + 0.33 DF - 0.33 DG - 0.33 DH - 0.33 EF - 0.33 EG - 0.33 EH - 0.33 FG + 0.33 FH + 0.33 GH - 0.33 BCD + 0.33 BCE - 0.33 BCF + 0.33 BCG + 0.33 BCH + 0.33 BDE + 0.33 BDF + 0.33 BDG - 0.33 BDH + 0.33 BEF - 0.33 BEG + 0.33 BEH - 0.33 BFG + 0.33 BFH - 0.33 BGH + 0.33 CDE + 0.33 CDF + 0.33 CDG + 0.33 CDH - 0.33 CEF - 0.33 CEG + 0.33 CEH + 0.33 CFG + 0.33 CFH + 0.33 CGH + 0.33 DEF - 0.33 DEG - 0.33 DEH + 0.33 DFG + 0.33 DFH + 0.33 DGH + 0.33 EFG - 0.33 EFH + 0.33 EGH + 0.33 FGH
An Added Bonus for Plackett-Burman Designs
But there is an added benefit to consider when using Plackett-Burman designs. Suppose that the effects that were not significant have been gradually eliminated from the model, and that only three main effects remain. With Plackett-Burman, you do not need to perform an additional 23 = 8-run full factorial design in order to estimate the two-factor interactions. The initial Plackett-Burman design already contains all the tests you need for this 23 full factorial design—and you will even get four replicates in addition to the full design!
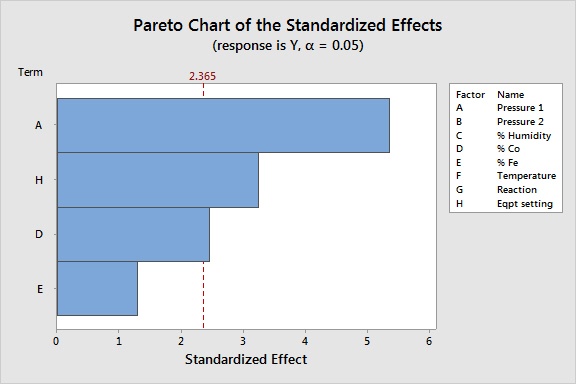
The Pareto diagram above from a Plackett-Burman design shows that only factors A, D & H have statistically significant effects.
Transforming a Plackett-Burman Design to a Full Factorial
To transform your Plackett-Burman design into a full factorial 23 design that will allow you to study all two-factor interactions in Minitab, go to Stat > DOE > Factorial > Define Custom Factorial Design... Select your three significant factors and click on Low/high to specify the factor settings. Now you can study the two-factor interactions.
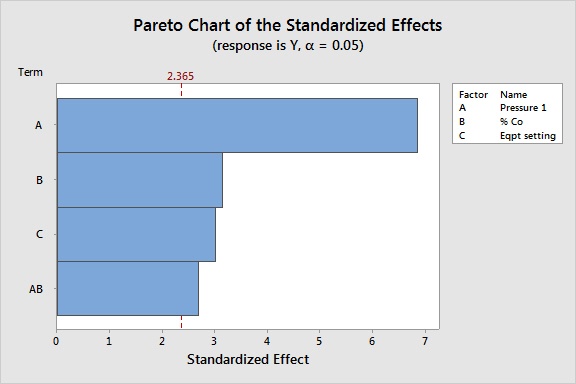
The initial Plackett-Burman design has been transformed into a full factorial design, the interactions between the three factors that have been previously selected can now be studied, and as we can see in the Pareto, graph one interaction appears to be statistically significant.
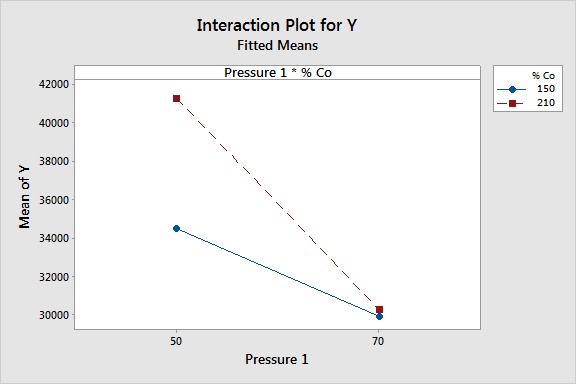
Of course, we can use Minitab to graph the significant interaction effect to get a better understanding of it.
Choosing the Right Experimental Design for Your Needs
Experimenters need to identify the best trade-off between running a limited number of tests and getting as much information as possible to improve processes / products. Plackett-Burman designs act as a funnel, enabling a quick reduction in the number of potential factors.
That is the reason why, in the Minitab Assistant, Plackett-Burman screening designs are considered when the number of potential factors is greater than five. After the analysis phase of the DOE results, if the number of significant factors in a 12-run Plackett-Burman design is equal to or smaller than 3, the initial design may easily be transformed into a full factorial DOE enabling you to study all two-factor interactions.


