Allow me to make a confession up front: I won't hesitate to beat my kids at a game.
My kids are young enough that in pretty much any game that is predominantly determined by skill and not luck, I can beat them—and beat them easily. This isn't some macho thing where it makes me feel good, and I suppose is only partially based in wanting them to handle both winning and losing well. It's just how I play, and in any event most kids games are designed with enough luck that a young child has a chance to beat an adult. I've observed other parents who let their kids win at these games of skill—maybe not every time, but enough to make the game seem more fair than it really is.
For both me and my bigger-hearted friends, Chutes and Ladders is a fantastic game. Why? It's not 10% luck, or 50%, or even 90% luck. Chutes and Ladders is 100% luck. You can't be good at it or bad at it. You can't try to win or lose. I can have no mercy and want to win as much as anything and it won't help me at all. And a parent who can't stand the idea of beating a kid at a game can (I hope) let that stress go, because they couldn't let their opponent win if they wanted to.
Modeling human decision-making with statistics can be very tough. If I wanted to make a simulation of three people playing Monopoly, for example, you can imagine the complexity in doing so accurately. But modeling a game like Chutes and Ladders is much easier. So much easier, in fact, that I went ahead and did it in Minitab Statistical Software using a concept known as Markov Chains.
So let's learn a little bit about the odds associated with Chutes and Ladders...
How the Odds Work in Chutes and Ladders
Here is a standard Chutes and Ladders board:
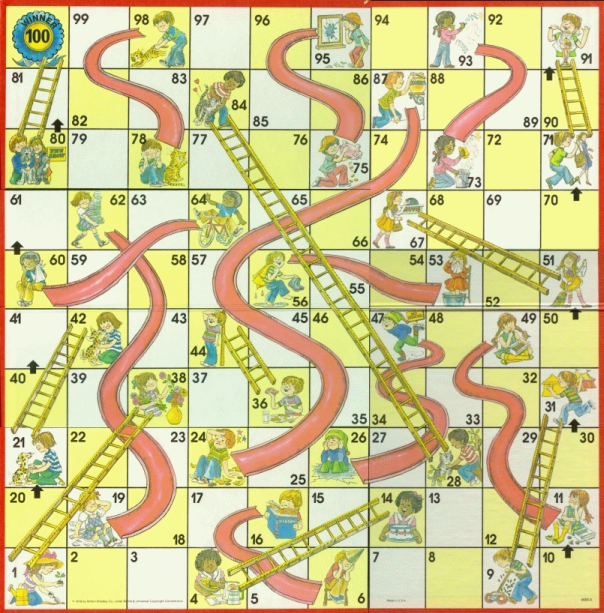
The game is simple: you roll a die (or use a spinner) that we can assume gives you an equal probability of obtaining a 1, 2, 3, 4, 5, or 6, and that's the number of spaces you move from your current position. If you stop on a space with a ladder that extends up, you go up the ladder. If you stop on a space with a chute that goes down, you descend. Ultimately, you must land exactly on the 100 space to win the game.
The Fastest (and Slowest) Win
The fewest turns you can possibly use to reach the 100 space is 7, and this only occurs in 0.151% of player-games, or about 1 in 622. Now those are the odds for each player—if you have multiple players in the game (and I hope no one plays Chutes and Ladders alone), then the odds are higher that at least one player finishes in the minimum 7 moves. Specifically, the odds are 1-(1-0.00151)n, where n is the number of players. For example, with three players the odds have jumped to a whopping 0.452%, or about 1 in 221 games.
Technically you could have an unlimited number of turns without ever reaching the 100 space, so there is no theoretical "most" turns it can take. But obviously as you take more turns, the odds of not winning keep decreasing. So instead let's just look at some cutoffs:
- 90% of player-games will finish before turn 72
- 95% of player-games will finish before turn 89
- 99% of player-games will finish before turn 128
Again, that's for just one player. For multiple players here is a graph of how many spins there are until a winner and the odds:
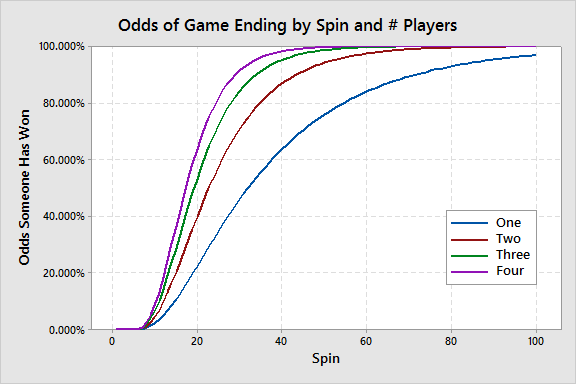
So if you're not looking for a drawn-out game, it helps immensely to recruit more players! With four players, the 99th percentile drops from 128 spins to just 44 spins.
How Many Moves Are Expected?
Now that the extreme cases have been covered, consider the more basic question of how many moves are expected before the game is won. First it's worth considering whether an expected value - the mean - is truly desired, or the median value. For one player, it is simple to answer both:
- The mean number of moves before a single player wins is about 39.
- The median number of moves is 32.
Based on this it can be seen that the distribution of moves is skewed right and the extremely long games are raising the mean number of moves well above the median.
But what about a game with more than one player?
- A game with two players would end in a median 23 moves and a mean 26.3 moves.
- A game with three players would end in a median 20 moves and a mean 21.7 moves.
- A game with four players would end in a median 18 moves and a mean 19.3 moves.
As the central limit theorem would predict, the distribution becomes less skewed as the number of players increases, and therefore the mean is closer to the median. So while increasing players decreases the median number of moves only a little bit, it greatly reduces the chances that a game will require a large number of turns.
All Spaces Are Not Created Equally
I once found myself maybe 20 spins into a game, and yet still on the bottom row. Space 6, to be exact. Not surprisingly, if you examine the board above, you find a chute that ends on space 6. As it turns out, not only is there a path that can get you all the way to the 100 spot in just a few spins, there is also a path that can be devastating. Specifically, you can take a spin while on space 97, and within a few spins find yourself back to space 6 thanks to an unfortunate series of chutes.
The chutes and ladders on the board mean some spaces are much more likely to have a player on them at any given time than others. Consider a ladder: there are multiple spaces you can spin from and land at the bottom of a particular ladder, but everyone who lands on that ladder ends up on the same spot. To illustrate the distribution of spaces occupied after a certain number of spins by a single player, I created a bubble plot where the size of each bubble corresponds to the probability of a player being on that space after each of the first 40 spins:
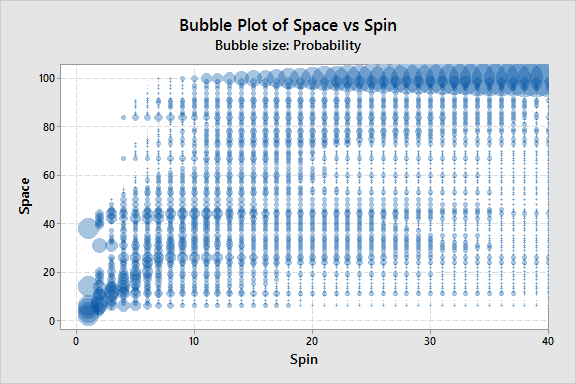
From the plot it can be seen that although the odds are low, even after 40 spins you might find yourself still on space 6. Rows of bubbles larger than those around them correspond to the end points of the various chutes and ladders, giving them higher probability than other points.
A Statistician's Take on Chutes and Ladders
While certain games like blackjack or poker might allow a player to improve their ability by understanding the odds, Chutes and Ladders is entirely based on luck and no such advantage can be gained. However, that doesn't mean there is nothing to learn by examining them. For example, if you really dislike the game but have a young child who always wants to play, you now know that encouraging another parent or a sibling to join in can really help prevent a never-ending game!
Game-play photo by Ben Husmann, used under Creative Commons 2.0.



