It sometimes may be prohibitively expensive or time-consuming to gather data for all runs for a designed experiment (DOE).
For example, a 6 factor, 2-level factorial design can entail 64 experimental runs, which may be too high a number for your particular situation. We have seen how to handle these some of these situations in previous posts, such as Design of Experiments: "Fractionating" and "Folding" a DOE and Gummi Bear DOE: Selecting Your Experimental Design Resolution. Both of these articles discuss how to create a smaller subset of your design and what to look out for when doing so.
What would we do if we wanted to minimize a response surface design, though?
What Is a Surface Response Design?
A response surface design is used when you suspect curvature in the response. It allows you to add squared (or quadratic) terms to your model in order to analyze that curvature.

A central composite design, one type of RSD, consists of:
-
Factorial Cube points
-
Axial points (values outside of cube’s low and high)
-
Center points. (values in the middle of the cube)
A central composite design with two factors is shown below. Points of the diagram represent the experimental runs that are performed:
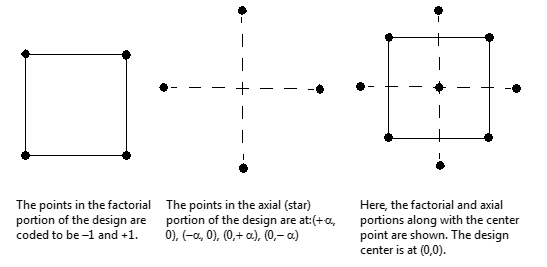
You may already be saying, “but my existing factorial design also can contain cube and center points.” That is true. Your factorial design, however, can only attempt to detect curvature in your model—it can’t necessarily model it. This is where response surface designs come in to save the day.
If curvature is detected in the response surface, you can modify your existing factorial design into an RSD by adding axial points in order to analyze a model with quadratic terms. (In Minitab Statistical Software, you can do this by going to Stat > DOE > Factorial Design > Modify Design > Add Axial Points). This allows you to build upon your design without having to create a RSD from scratch.
Reducing Your RSD
There are a couple of ways you can reduce the size of your central composite design if you deem it too large.
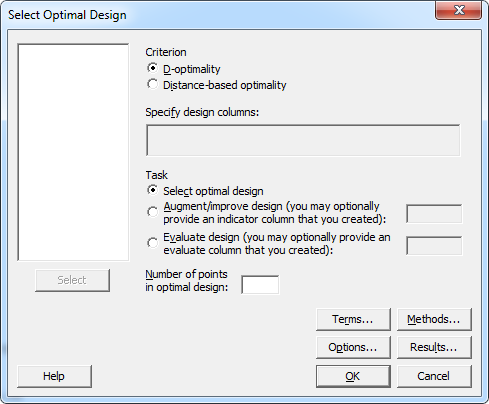
1. Select Optimal Design
Minitab can use one of two methods for reducing your design, D-Optimality and Distance Based Optimality. D-Optimality does require that you have an idea of what terms in the model (certain interactions, squares) you’ll eventually want to analyze. You’ll specify those terms under the “Terms” sub-menu. Distance Based, however, can be used when you don’t have the ability to specify a model in advance.
For either method, you will have to specify the number of runs in your reduced design as well, in the box labeled “Number of points in your optimal design.” You can find Select Optimal Design under Stat > DOE > Response Surface > Select Optimal Design.
2. Fractional Response Surface Designs
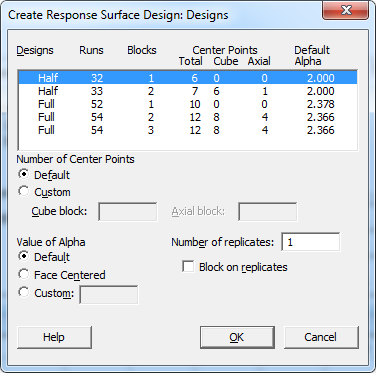
Surprise! Yes, you can take a fraction of your RSD, but the availability of fractionating your design depends on the amount of continuous factors you are analyzing. Please view the chart below:
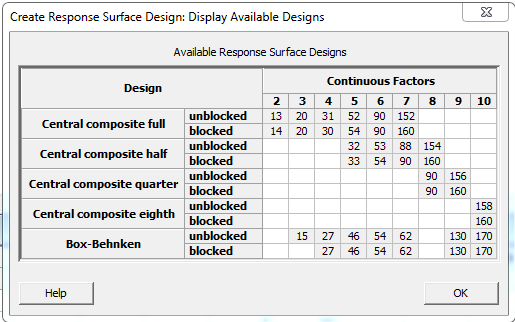
The values in the table represent the total number of runs that will be created each type of design. For a 5-factor, ½-fraction central composite design, either 32 or 33 runs will be created, depending on whether it’s blocked.
One difference between a fractional factorial and a fractional CCD is that the CCDs are all resolution V or better. All of the main effects, 2-factor interactions and square terms can be estimated independently of each other. Since those are the only terms we consider in response surface models, we do not show the alias table that we are normally accustomed to seeing when creating a fractional factorial design. The alias table would display the terms that cannot be estimated independently of one another.
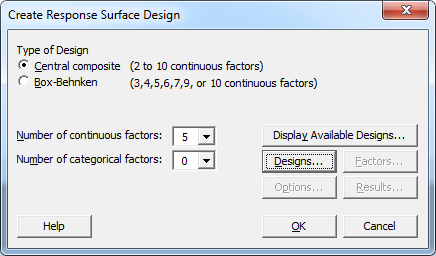
You can create a fractional response surface design under Stat > DOE > Response Surface > Create Response Surface Design. If you have at least 5 factors, you’ll have the option to take a half-fraction design under the Designs sub-menu.
I hope this information helps you when you create your next DOE!



