Are you someone who never imagined you’d be using statistics in your work? Do you feel, at times, like an undercover interloper in the land of p-values, as you step gingerly to avoid statistical land mines with long, complex-sounding names?
For example, do you feel a slight chill run down your spine when you read:
“For your analysis results to be valid, you should ascertain whether your data satisfy the assumption of homoscedasticity”?
Sometimes it’s best to face your fears head on.
Granted, homoscedasticity is definitely not a word you should say in public with a mouthful of beer and mashed potatoes. But, like a lot of high-falutin’ specialized terminology, it’s actually much simpler than it appears.
Take a look at its Greek roots.

So, homoscedasticity literally means“ having the same scatter.” In terms of your data, that simply translates into having data values that are scattered, or spread out, to about the same extent.
Homoscedasticity: Why the Big Word for this Simple Concept?
Homoscedasticity is a formal requirement for some statistical analyses, including ANOVA, which is used to compare the means of two or more groups. This requirement usually isn’t too critical for ANOVA--the test is generally tough enough (“robust” enough, statisticians like to say) to handle some heteroscedasticity, especially if your samples are all the same size. However, if you want to compare samples of different sizes, you run a much greater risk of obtaining inaccurate results if the data is not homoscedastic.
Luckily, Minitab has a lot of easy-to-use tools to evaluate homoscedasticity among groups.
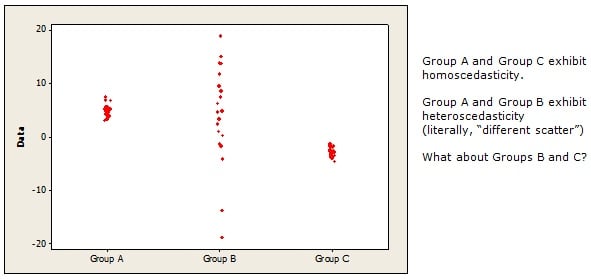
Individual Value Plot
If you have small samples, you can use an Individual Value Plot (shown above) to informally compare the spread of data in different groups (Graph > Individual Value Plot > Multiple Ys). Just eyeball the data values to see if each group has a similar scatter.
Boxplot
For larger data sets, use boxplots to informally compare the spread of data in different groups (Graph > Boxplot > Multiple Ys).
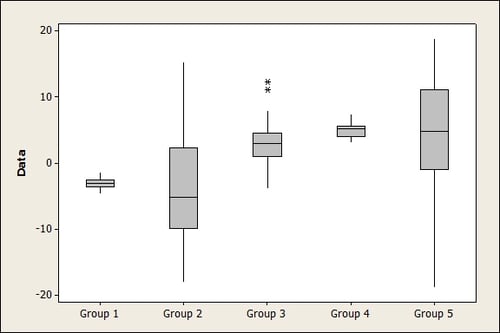
Which pairs of groups above appear roughly homoscedastic? Which heteroscedastic?
Hint: Remember, the location of the boxplots isn't the issue here—just whether they have about the same spread, as indicated by the lengths of their boxes and "whiskers." (For more info on interpreting boxplots, choose Help > Glossary and click Boxplot from the index of terms.)
Descriptive Statistics
The variance is a statistic used to measure how spread out (scattered) the data are. To calculate the variance, choose Stat > Basic Statistics > Display Descriptive Statistics, click Statistics, and check Variance.
Here are the variances for the first three groups shown on the boxplot above.

The larger the variance, the greater the scatter, or spread, of the data. So Group 2 has the greatest spread and Group 1 has the least amount of spread.
To evaluate homoscedasticity using calculated variances, some statisticians use this general rule of thumb: If the ratio of the largest sample variance to the smallest sample variance does not exceed 1.5, the groups satisfy the requirement of homoscedasticity. Using the variances calculated above, that ratio is 58.14/0.7 = 83.05. So Groups 1, 2, and 3 definitely don’t meet the requirement—they're heteroscedastic.
Test for Equal Variances
To more rigorously compare the scatter of data in two or more groups, you can formally test the variances to see whether they statistically differ. Choose Stat > ANOVA > Test for Equal Variances.
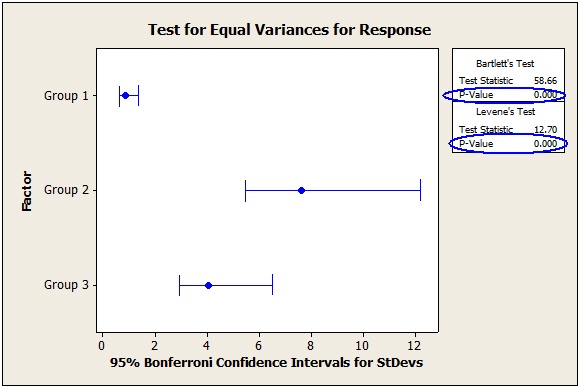
Minitab performs two tests to determine whether the variances differ. Use Bartlett’s test if your data follow a normal, bell-shaped distribution. If your samples are small, or your data are not normal (or you don’t know whether they’re normal), use Levene’s test.
If the p-value is less than the level of significance for the test (typically, 0.05), the variances are not all the same. In that case, you can conclude the groups are heteroscedastic, as they are in the output above. (Notice that this matches the results for these 3 groups when using the rule-of-thumb test and the boxplots.)
Be unafraid. Be very, very unafraid.
In conclusion, then, it does not behoove you to permit extreme trepidation and apprehension to emanate from your amygdala when confronted with an egregious predilection for prolix exposition and inveterate hippopotomonstrosesesquipedalianism. (Translation: Don’t let big words scare you.)
Homoscedasticity, equal variances, homogeneity of variance—they’re all just fancy ways of saying “same scatter.”



