These days, my memory isn't what it used to be. Besides that, my memory isn't what it used to be.
But my incurable case of CRS (Can't Remember Stuff) is not nearly as bad as that of the exponential distribution.
When modelling failure data for reliability analysis, the exponential distribution is completely memoryless. It retains no record of the previous failure of an item.
That might sound like a bad thing. But this special characteristic makes the distribution extremely useful for modelling the behavior of items that have a constant failure rate.
Using the Exponential Distribution to Model Failure Data
Suppose you track the time until failure of a randomly collected sample of items. When you graph the results on a histogram, you get something like this:
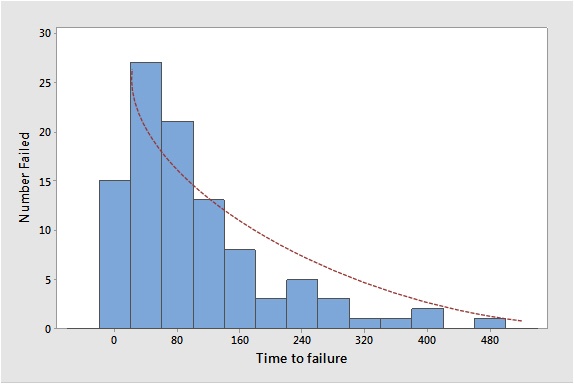
Notice that the number of items that fail at a given point in time decreases steadily as time elapses. This steady decrease can be fit nicely to an exponential curve.
Because the decrease is steady, if you were to plot the instantaneous risk of failure for any item at any specific point in time (t)—what's known as its hazard function—you'd end up with a constant risk of failure at any point in time:

The failure of an item at any point previously does not affect the risk of failure at any other point in time. That means the exponential distribution has the good fortune of not being able to "remember" any of its past failures. (Every day is a brand new day, if you're exponentially distributed! No baggage!)
For this reason, the exponential distribution often provides a good model in reliability analysis for a product or part that is just as likely to fail at any time, regardless of whether it is brand new, a year old, or several years old. Such an item is not expected to age or wear out over its intended application (such as a component in a product that doesn't typically wear out until long after the product itself does).
However, if a component is expected to show fatigue, corrosion, or wear before the expected life of the product is complete, then the exponential distribution is not a good model, because the risk of failure increases over time.
Choosing a Distribution: Practical Know-How + P-Plots
The exponential distribution is just one of several distributions that are commonly used to model failure data in reliability analysis. Selecting a distribution that models your data well is a critical requirement for the analysis.
You can use Minitab's Distribution ID plots to evaluate the fit of various distributions (Stat > Reliability/Survival > Distribution Analysis...) If the points fall in a straight line along the fitted distribution line, the distribution may provide a good fit.
The plots below show that the exponential distribution is clearly a better fit for the failure data than the normal distribution.
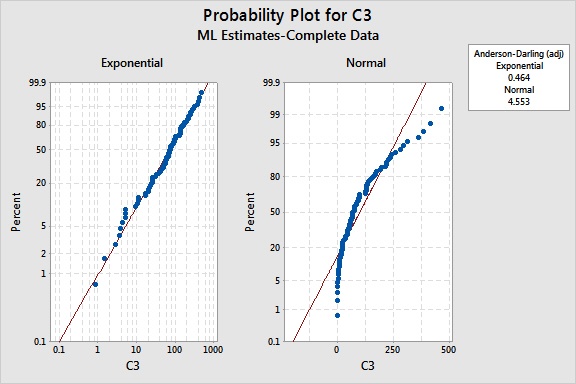
When using probability plots, it's possible that several distributions may provide a good fit for your data. So it's also helpful to be familiar with the defining characteristics and common applications of the distributions when making your decision.
Already Forgot What You Just Read?
Luckily, you don't have to memorize all the characteristics of each distribution. Instead, save the precious space in your brain to remember Mother's Day, and bookmark this in-depth explanation on Minitab Support: Exponential Distribution in Reliability Analysis.
Case study:
Time-to-Market and Design for Reliability at the Speed of Light in Signify
Get ready for a light bulb moment! In a fast-changing industry where time-to-market and product reliability give a competitive edge, discover how the world’s leading lighting company Signify, rapidly validates new innovations. In this one hour webinar, Prof W.D. van Driel and Dr P. Watté will shed a light on design for reliability (DfR) using Minitab Statistical Software at Signify, the former Philips Lighting. Learn from real-life examples their methods to lower your development costs, improve your designs’ performance and compliance, and accelerate the testing of product design reliability. If you develop products intended to meet high specifications for years to come, you will discover how to reduce the risks and consequences of product failure and costly claims - for you and your customers.





![[Webinar Replay] Time-to-Market and Design for Reliability at the Speed of Light at Signify](https://no-cache.hubspot.com/cta/default/3447555/b70a5a3e-03b6-408b-bbc1-7851ef13e4e9.png)