Now that we've explored all of the DOE design choices in Minitab Statistical Software, it's time to think about the levels of the factors. I chose these 5 factors previously:
- Position of catapult on the launch ramp
- Angle of catapult
- Number of rubber band windings
- Position of gummi bear on the catapult
- Position of fulcrum in the catapult
What Is an Effect in DOE?
In DOE, we're trying to detect the effect of changing each variable from the low to high level. Usually, the way to make the difference most obvious is to make the levels as far apart as possible. Let me borrow some data from Carly Barry to illustrate the idea in two dimensions. Here is a Fitted Line Plot that shows the relationship between the year an Olympics was held and the 100m dash times for the medal winners.
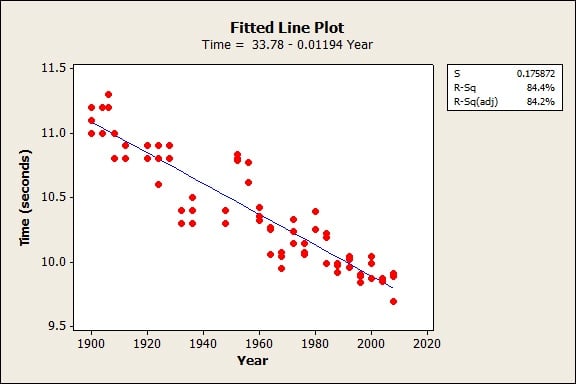
The effect is the change in the response variable when we go from the low level of the factor to the high level of the factor. The farther apart the levels are, assuming a linear relationship, the bigger the effect is. In Carly's data, if the high and low level were 1 year apart, the average effect would be about 1/100 of a second. If we made the high and low levels 100 years apart, the effect would be about 1 second. As we saw when we did the power calculations, the larger the effect is, the more likely we can determine that the effect is statistically significant.
(Okay, so it's not Matt Cassell knee pain, but it does hurt.)
Levels for the Gummi Bear DOE
Because we want the numeric factor levels to be as far apart as possible in DOE, the best we can do is to use the minimum and the maximum for the low and high levels. This works nicely for the position of the catapult on the launch ramp. Put the catapult at the bottom of the ramp and at the top of the ramp.
For number of rubber band windings and angle of catapult, the level choices require some experimentation. With my materials, I have to wind the rubber band 3 times to get a gummi bear to launch. I can wind the rubber band 8 times, but it hurts my fingers and I imagine that doing it 48 times would become physically unpleasant. So my levels are going to be 3 and 7. The choice of two odd numbers (or two even numbers) will simplify matters when I collect center points. I won't have to choose what to do when the center point is 5.5 windings!

For the angle of the catapult, setting the launch ramp flat is an obvious minimum for the low level. The high level presents difficulties. 360 degrees is the same as 0, and 180 degrees would launch the gummi bear straight into the ground. A setting of 90 could have been a good choice, but sadly for spreading out my levels, gummi bears do not defy gravity for the sake of statistics experiments. To me, it looks like the high level will have to be 16 degrees. It will be interesting to see whether that's enough of a change to have on effect on how far the gummi bears fly!
The position of the fulcrum and the position of the gummi bear are complicated because the gummi bear has to be above the fulcrum or it won't launch. The wider we make the fulcrum levels, the narrower the gummi bear levels have to be. I'm going to try the mid-point of the popsicle stick as the high point for both.
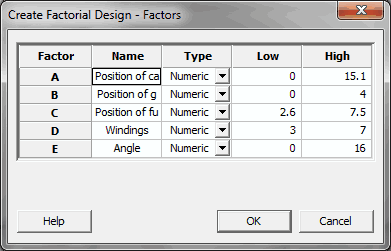
Here's how I completed the factors for the DOE in Minitab:
Can't wait for more statistics? Intrigued by Carly's running data? Check out our other analyses of the 2012 Olympic games!
Meteorology and the Triple Jump
Men’s 100m Dash: How have the times changed over the years?
Visualizing the Greatest Olympic Outlier of All Time
Identical Twins, Rowing, and the Luck of the Lane
When Even Cupid Isn't Accurate Enough: Interval Plots and Olympic Finals
Has Figure Skating Judging Improved? What Do the Numbers Say?



