Last time, we used stepwise regression to come up with models for the gummi bear data. Stepwise regression is a great tool, but it has a downside: when we use stepwise selection in design of experiments, especially if we focus on only the last step, we can miss interesting models that might be useful.
One way to look at more models is to use Minitab’s Best Subsets feature. Instead of identifying a single model based on statistical significance, Minitab’s Best Subsets feature shows a number of different models, as well as some statistics to help us compare those models.
To get the idea, let’s look at some smaller models.
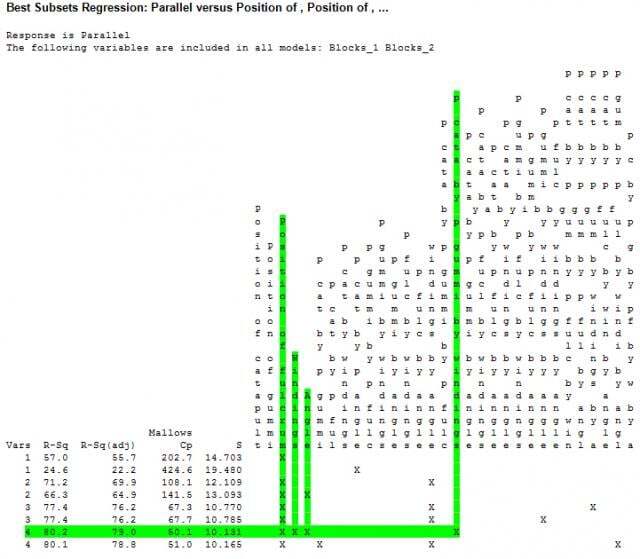
The variables column (Vars) shows how many terms are in the model. In this case, I requested that Minitab print two models with 1–4 terms. Here are the statistics that Minitab provides to help you choose a model:
- R2 is for when you compare models with the same number of terms. Higher is better.
- Adjusted R2 is for when you compare models with different numbers of terms. Higher is better.
- Mallows’ Cp is for when you compare models with the same or different numbers of terms, provided all of the models came from the same initial set of terms. If you change the predictors and run best subsets a second time, you cannot use Mallows’ Cp to compare the models. The smaller the Mallows’ Cp, the better it is for prediction. The closer it is to the printed number of variables + 1 (for the intercept term), the less biased the estimates of the coefficients are.
- S is an estimate of the variability about the regression line. Smaller is better.
In the output above, the model with
- the position of the fulcrum
- the angle of the catapult
- the number of rubber band windings, and
- the interaction between the position of the catapult, the position of the gummi bear, and the number of rubber band windings
has the best statistics. However, the statistics for the other 4-predictor model are so close that it would be hard to say that one is practically better than the other.
With a smaller number of models to work with, you can use Minitab to check the predicted R2 values. Predicted R2 is similar to the other R2 type statistics, but estimates how well a model predicts new observations. Often, this criterion about new observations is the most appealing assessment to use. We want the model to predict what will happen when we launch a new gummi bear. As it turns out, the predicted R2 values are nearly equal for both four-term models: 77.09%. Based on these statistics, there’s no reason to think that one model will outperform the other, even though their predictions can vary considerably.
Next time, I’ll plan to take a look at some larger models to see if we can do better on the predictions. If you’re ready for more statistics now, take a look at what Jim Colton can show you about some common misconceptions about R2.



