For hundreds of years, people having been improving their situation by pulling themselves up by their bootstraps. Well, now you can improve your statistical knowledge by pulling yourself up by your bootstraps. Minitab Express has 7 different bootstrapping analyses that can help you better understand the sampling distribution of your data.
A sampling distribution describes the likelihood of obtaining each possible value of a statistic from a random sample of a population—in other words, what proportion of all random samples of that size will give that value. Bootstrapping is a method that estimates the sampling distribution by taking multiple samples with replacement from a single random sample. These repeated samples are called resamples. Each resample is the same size as the original sample.
The original sample represents the population from which it was drawn. Therefore, the resamples from this original sample represent what we would get if we took many samples from the population. The bootstrap distribution of a statistic, based on the resamples, represents the sampling distribution of the statistic.
Bootstrapping and Running Backs
For example, let’s estimate the sampling distribution of the number of yards per carry for Penn State’s star running back Saquon Barkley. Going through all 182 of his carries from last season seems daunting, so instead I took a random sample of 49 carries and recorded the number of yards he gained for each one. If you want to follow along, you can get the data I used here.
Repeated sampling with replacement from these 49 samples mimics what the population might look like. To take a resample, one of the carries is randomly selected from the original sample, the number of yards gained is recorded, and then then that observation is put back into the sample. This is done 49 times (the size of the original sample) to complete a single resample.
To obtain a single resample, in Minitab Express go to STATISTICS > Resampling > Bootstrapping > 1-Sample Mean. Enter the column of data in Sample, and enter 1 for number of resamples. The following individual plot represents a single bootstrap sample taken from the original sample.
Note: Because Minitab Express randomly selects the bootstrap sample, your results will be different.
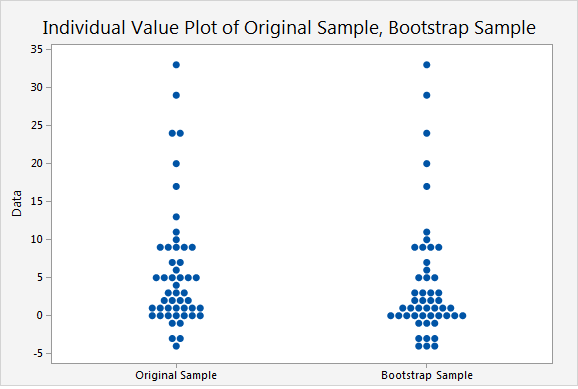
The resample is done by sampling with replacement, so the bootstrap sample will usually not be the same as the original sample. To create a bootstrap distribution, you take many resamples. The following histogram shows the bootstrap distribution for 1,000 resamples or our original sample of 49 carries.
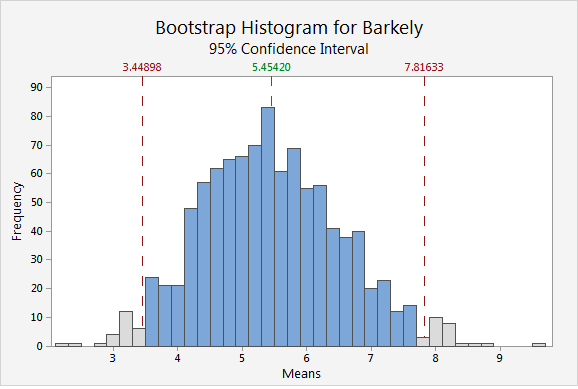
The bootstrap distribution is centered at approximately 5.5, which is an estimate of the population mean for Barkley’s yards per carry. The middle 95% of values from the bootstrapping distribution provide a 95% confidence interval for the population mean. The red reference lines represent the interval, so we can be 95% confident the population mean of Barkley’s yards per carry is between approximately 3.4 and 7.8.
Bootstrapping and the Central Limit Theorem
The central limit theorem is a fundamental theorem of probability and statistics. The theorem states that the distribution of the mean of a random sample from a population with finite variance is approximately normally distributed when the sample size is large, regardless of the shape of the population's distribution. Bootstrapping can be used to easily understand how the central limit theorem works.
For example, consider the distribution of the data for Saquon Barkley’s yards per carry.
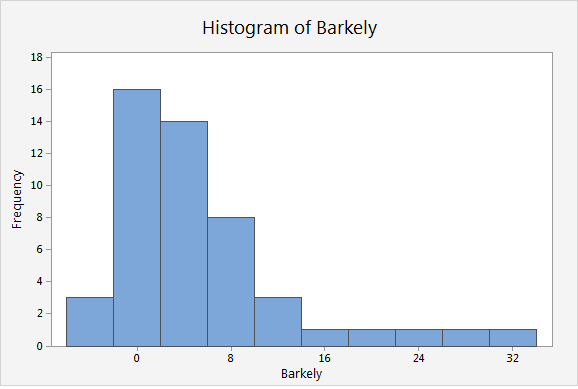
It’s pretty obvious that the data are nonnormal. But now we’ll create a bootstrap distribution of the means of 10 resamples.
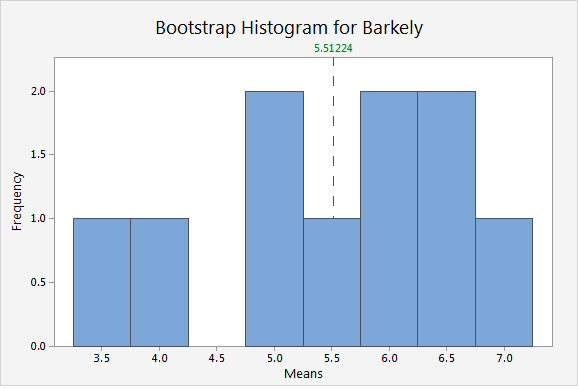
The distribution of the means is very different from the distribution of the original data. It looks much closer to a normal distribution. This resemblance increases as the number of resamples increases. With 1,000 resamples, the distribution of the mean of the resamples is approximately normal.

Note: Bootstrapping is only available in Minitab Express, which is an introductory statistics package meant for students and university professors.



