Choosing the Right Distribution Model for Reliability Data

Recently I've been refreshing my knowledge of reliability analysis, which is the use of data to assess a product's ability to perform over time. Quality engineers typically use reliability analysis to predict the likelihood that a certain percentage of products will fail over a given amount of time.

Statistical software will do the calculations involved in a reliability analysis, but there's a catch: first, you must choose a distribution to model your data. Put plainly, you need to tell the software to base its analysis on the normal distribution, the Weibull distribution, or perhaps some other, more exotic distribution.

Why does choice of distribution matter for reliability analysis?

Let's say you work for a company that makes engine windings for turbines. You're concerned that if these parts are exposed to high temperatures, they will fail at an unacceptable rate. You want to know -- at given high temperatures -- the time at which 1% of the windings fail.

First you collect failure times for the parts at two temperatures. In the first sample, you test 50 windings exposed to 80 °C; in the second sample, you test 40 items at 100 °C.

Naturally, you want your reliability analysis to be...um... reliable. This is where choosing the right distribution comes in. The more closely the distribution fits your data, the more likely the results of the reliability analysis will provide good information about how your product will perform.

You want to use parametric distribution analysis to assess the reliability of the engine windings. But how do you know which distribution to choose for your data?

Using statistical software to identify the distribution of reliability data

Textbooks suggest relying on practical knowledge or direct experience with product performance. You might be able to identify a good distribution for your data by answering questions such as:

Do the data follow a symmetric distribution? Are they skewed left or right?
Is the failure rate rising or falling? Or is it staying constant?
What distribution has worked for this analysis in the past?

If you don't have enough knowledge or experience to confidently select a distribution, statistical software can help. In Minitab, we can evaluate the fit of our data using the Distribution ID plot, by choosing Stat > Reliability/Survival > Distribution Analysis (Right-Censoring or Arbitrary Censoring).

This tool lets us determine which distribution best fits the data by comparing how closely the plot points follow the best-fit lines of a probability plot. We'll choose the Right-Censoring option and fill out the dialog box as shown:

We're just going to compare our data to the Weibull, Lognormal, Exponential, and Normal distributions; however, had we wished, we could have Minitab test the fit of our data against 11 distributions by clicking the "Use all distributions" option.

When we click "OK," Minitab gives us a lot of output in the Session window, and also this graph:

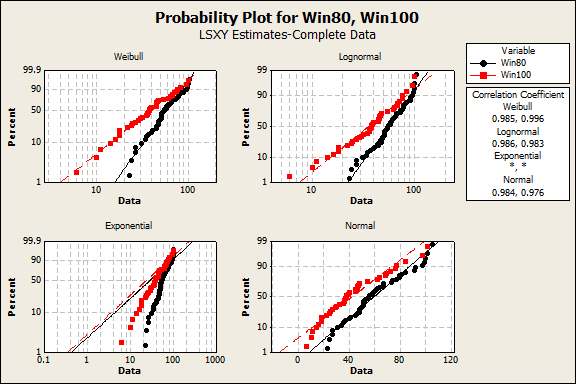
Choosing the best distribution model from the identification plot

We're looking to see which distribution line is the best match for our data. Immediately we can rule out the Exponential distribution, where barely any of our data points follow the best-fit line. The other three look better, but the points seem to fit the straight line of the lognormal plot best, so that distribution would be a good choice for running subsequent reliability analyses.

It can sometimes be difficult to tell which distribution is the best fit from the graph, so you should also check the Anderson-Darling goodness-of-fit values and other statistics in the Session window output. The Anderson-Darling values appear alongside the "Correlation Coefficients" on the plot. The smaller the Anderson-Darling value, the better the fit of the distribution.

For our data, the Anderson-Darling value for the lognormal distribution is lower than those for other distributions, further supporting the lognormal distribution as the best fit.

Have you ever needed to identify the distribution of your data? How did you do it?

Case study:
Time-to-Market and Design for Reliability at the Speed of Light in Signify

Get ready for a light bulb moment! In a fast-changing industry where time-to-market and product reliability give a competitive edge, discover how the world’s leading lighting company Signify, rapidly validates new innovations. In this one hour webinar, Prof W.D. van Driel and Dr P. Watté will shed a light on design for reliability (DfR) using Minitab Statistical Software at Signify, the former Philips Lighting. Learn from real-life examples their methods to lower your development costs, improve your designs’ performance and compliance, and accelerate the testing of product design reliability. If you develop products intended to meet high specifications for years to come, you will discover how to reduce the risks and consequences of product failure and costly claims - for you and your customers.

Choosing the Right Distribution Model for Reliability Data

Why does choice of distribution matter for reliability analysis?

Using statistical software to identify the distribution of reliability data

Choosing the best distribution model from the identification plot

Case study:Time-to-Market and Design for Reliability at the Speed of Light in Signify

You Might Also Like

Case study:
Time-to-Market and Design for Reliability at the Speed of Light in Signify