So the data you nurtured, that you worked so hard to format and make useful, failed the normality test.
Time to face the truth: despite your best efforts, that data set is never going to measure up to the assumption you may have been trained to fervently look for.
Your data's lack of normality seems to make it poorly suited for analysis. Now what?
Take it easy. Don't get uptight. Just let your data be what they are, go to the Stat menu in Minitab Statistical Software, and choose "Nonparametrics."
If you're stymied by your data's lack of normality, nonparametric statistics might help you find answers. And if the word "nonparametric" looks like five syllables' worth of trouble, don't be intimidated—it's just a big word that usually refers to "tests that don't assume your data follow a normal distribution."
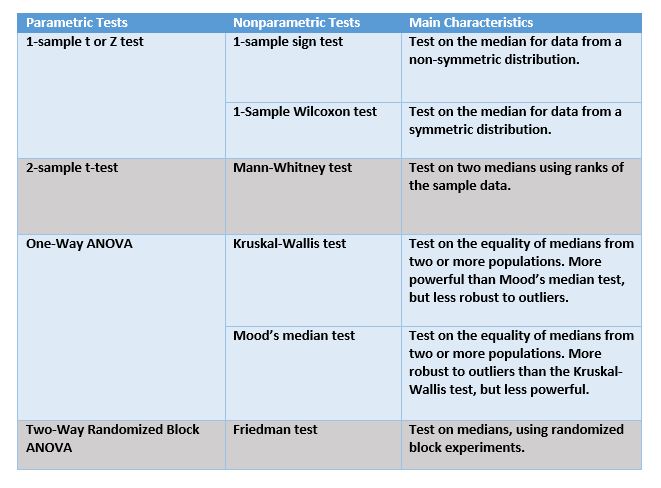
In fact, nonparametric statistics don't assume your data follow any distribution at all. The following table lists common parametric tests, their equivalent nonparametric tests, and the main characteristics of each.
Nonparametric analyses free your data from the straitjacket of the normality assumption. So choosing a nonparametric analysis is sort of like removing your data from a stifling, conformist environment, and putting it into a judgment-free, groovy idyll, where your data set can just be what it is, with no hassles about its unique and beautiful shape. How cool is that, man? Can you dig it?
Of course, it's not quite that carefree. Just like the 1960s encompassed both Woodstock and Altamont, so nonparametric tests offer both compelling advantages and serious limitations.
Advantages of Nonparametric Tests
Both parametric and nonparametric tests draw inferences about populations based on samples, but parametric tests focus on sample parameters like the mean and the standard deviation, and make various assumptions about your data—for example, that it follows a normal distribution, and that samples include a minimum number of data points.
In contrast, nonparametric tests are unaffected by the distribution of your data. Nonparametric tests also accommodate many conditions that parametric tests do not handle, including small sample sizes, ordered outcomes, and outliers.
Consequently, they can be used in a wider range of situations and with more types of data than traditional parametric tests. Many people also feel that nonparametric analyses are more intuitive.
Drawbacks of Nonparametric Tests
But nonparametric tests are not completely free from assumptions—they do require data to be an independent random sample, for example.
And nonparametric tests aren't a cure-all. For starters, they typically have less statistical power than parametric equivalents. Power is the probability that you will correctly reject the null hypothesis when it is false. That means you have an increased chance making a Type II error with these tests.
In practical terms, that means nonparametric tests are less likely to detect an effect or association when one really exists.
So if you want to draw conclusions with the same confidence level you'd get using an equivalent parametric test, you will need larger sample sizes.
Nonparametric tests are not a one-size-fits-all solution for non-normal data, but they can yield good answers in situations that parametric statistics just won't work.
Is Parametric or Nonparametric the Right Choice for You?
I've briefly outlined differences between parametric and nonparametric hypothesis tests, looked at which tests are equivalent, and considered some of their advantages and disadvantages. If you're waiting for me to tell you which direction you should choose...well, all I can say is, "It depends..." But I can give you some established rules of thumb to consider when you're looking at the specifics of your situation.
Keep in mind that nonnormal data does not immediately disqualify your data for a parametric test. What's your sample size? As long as a certain minimum sample size is met, most parametric tests will be robust to the normality assumption. For example, the Assistant in Minitab (which uses Welch's t-test) points out that while the 2-sample t-test is based on the assumption that the data are normally distributed, this assumption is not critical when the sample sizes are at least 15. And Bonnett's 2-sample standard deviation test performs well for nonnormal data even when sample sizes are as small as 20.
In addition, while they may not require normal data, many nonparametric tests have other assumptions that you can’t disregard. For example, the Kruskal-Wallis test assumes your samples come from populations that have similar shapes and equal variances. And the 1-sample Wilcoxon test does not assume a particular population distribution, but it does assume the distribution is symmetrical.
In most cases, your choice between parametric and nonparametric tests ultimately comes down to sample size, and whether the center of your data's distribution is better reflected by the mean or the median.
- If the mean accurately represents the center of your distribution and your sample size is large enough, a parametric test offers you better accuracy and more power.
- If your sample size is small, you'll likely need to go with a nonparametric test. But if the median better represents the center of your distribution, a nonparametric test may be a better option even for a large sample.



