In my last post, I showed how to use Minitab Statistical Software to create an acceptance sampling plan by variables, using the scenario of a an electronics company that receives monthly shipments of LEDs that must have soldering leads that are at least 2 cm long. This time, we'll compare that plan with some other possible options.
The variables sampling plan we came up with to verify the lead length called for the random selection and inspection of 64 items from each batch of 1,500 LEDs. You and the supplier agree that the AQL is 100 defectives per million and the RQL is 400 defectives per million. If the calculated Z value is greater than the critical distance (3.51320), you'll accept the entire lot. Sounds great, right?
But that's not what your boss thinks. He believes that inspecting 64 LEDs is a waste of time, and says he's got a gut feeling that you could probably get by with inspecting half of that number, maybe even fewer. Your gut tells you that's too low.
Fortunately, Minitab makes it easy to consider a few possible plans very easily, so neither of you need to place a bet on whose gut feeling is correct. If you'd like to follow along and you're not already using Minitab, please download the free 30-day trial.
Setting Up a Comparison of Acceptance Sampling Plans
Start by selecting Stat > Quality Tools > Acceptance Sampling by Variables > Create/Compare..., and when the dialog box appears, choose the option for Compare User Defined Sampling Plans.
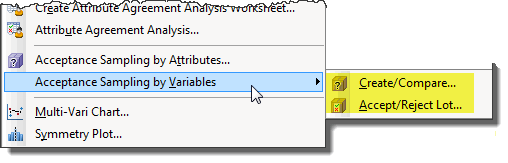
In Units for quality levels, choose Defectives per million. Since you and your supplier have already established the acceptable and rejectable quality levels, for Acceptable quality level (AQL) enter 100, and for Rejectable quality level (RQL or LTDP), enter 400. However, you don't need to enter AQL and RQL when you are simply comparing sampling plans.
In Sample sizes, enter 32 50 64 75 100, and enter 3.55750 in Critical distances (k values). All that's left is to enter the lower spec for each item, the historical standard deviation of .145, and the lot size of 1500.
When you press OK, Minitab's Session Window displays the following output:

How Do These Acceptance Sampling Plans Compare?
The table shown above shows the probabilities of accepting and rejecting lots of LEDs at quality levels of 100 and 400 defects per million opportunities for different sample sizes.
Your boss suggested cutting the number you sampled in half, to 32 items. Under that scenario, however, the producer's risk of having a good shipment rejected has more than doubled, from 5% to 12.2%. You know your supplier won't accept that. Moreover, your odds of properly rejecting a poor-quality shipment have fallen from 90% to just 81%, a level you aren't comfortable with. It's clear that a sample size of 32 does not give you or supplier sufficient protection.
Minitab also produces graphs that make it easy to see and understand the differences between sampling plans visually. In the graph below, the solid blue line represents the 32-item sampling plan, the dotted red line represents a plan that samples 50 items, and the green line represents the original sampling plan you devised, which called for evaluating 64 items.
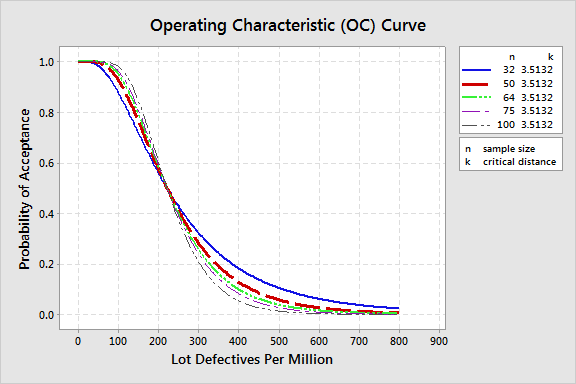
Comparing these curves, it's easy to see how far the blue line representing a 32-item sample diverges from the others. But the lines for the 50- and 64-item sampling plans are quite close; the chance of rejecting a good lot only rises 2%, from 5 to 7%, while the odds of correctly rejecting a poor lot only fall 3%, from 90 to 87%.
Evaluating 14 fewer LEDs would save a fair amount of time without adding much additional risk for either your or your supplier, so the 50-item sampling plan may be the best option for keeping yourself, your supplier, and your boss amenable to the inspection process.
In my next post, we'll use that sampling plan to evaluate the next lot of 1,500 LEDs, and make a decision about whether to accept the shipment, or reject it and return it to the supplier for corrective action.



