In the last post, we discussed how general full factorial designs let you study factors at more than two levels. The remaining 4 options that Minitab offers for factorial design of experiments are all 2-level designs, including the Plackett-Burman design.
Because there are 4 different kinds of 2-level designs, one of which is selected by default, you can probably guess that 2-level designs are quite popular. So what’s special about a 2-level design, and why would we use one?
One of the benefits of using design of experiments to plan data collection is to learn as much as possible from the smallest amount of data. One important method to achieve this benefit is sequential experimentation: we collect some data to find out if we have to collect more data. That way, we don’t collect data more data than we need. The basic idea of a 2-level design is that by collecting data at only 2 levels, we learn the same thing as if we collected data at lots of levels, presuming the relationship between our variables is linear.
The Journal of the American Academy of Dermatology has published a report about how high SPF sunscreen can protect people who don't put apply enough sunscreen to achieve the advertised SPF. The authors conclude that, for high SPF suncreens, there is a linear relationship between the advertised SPF of a sunscreen and the actual SPF a person gets when they apply a thickness of 0.5 mg/cm2. We could test lots of special sunscreens with SPF values between 70 and 100 to get a good picture of what’s happening for all SPF values. Or, because the relationship is linear, we could collect data only about sunscreens with SPFs of 70 and 100 and get almost the exact same information.
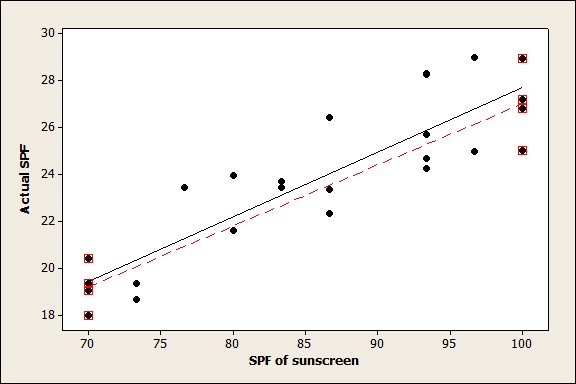
This is an invented graph, not the real data from the study. The red line, drawn to fit just the 8 points with red squares around them, is almost the same as the black line drawn to fit all 25 points.
The more time-consuming and expensive it is to measure a factor at different levels, the more valuable it is to learn more from less data.
But what if we don’t know that the relationship is linear? Then we can simply add “center points” to our 2-level design. It means that we have to collect data at one more level, but the level is chosen to give us the most information about potential curvature in the data. It’s worth knowing that although they’re called “2-level” designs, Minitab will add a third level that lets you check whether or not the relationship is linear. When you're building your confidence in choosing a method for design of experiments, it's nice to know that Minitab is going to take care of you like that.
The image of the surfer, by Jon Sullivan, is from Public domain images.



