How Many Samples Do You Need to Be Confident Your Product Is Good?

How many samples do you need to be “95% confident that at least 95%—or even 99%—of your product is good?

The answer depends on the type of response variable you are using, categorical or continuous. The type of response will dictate whether you 'll use:

1. Attribute Sampling: Determine the sample size for a categorical response that classifies each unit as Good or Bad (or, perhaps, In-spec or Out-of-spec).
    
2. Variables Sampling: Determine the sample size for a continuous measurement that follows a Normal distribution.

The attribute sampling approach is valid regardless of the underlying distribution of the data. The variables sampling approach has a strict normality assumption, but requires fewer samples.

In this blog post, I'll focus on the attribute approach.

Attribute Sampling

A simple formula gives you the sample size required to make a 95% confidence statement about the probability an item will be in-spec when your sample of size n has zero defects.

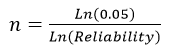, where the reliability is the probability of an in-spec item.

For a reliability of 0.95 or 95%,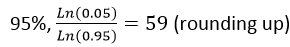

For a reliability of 0.99 or 99%,  

Of course, if you don't feel like calculating this manually, you can use the Stat > Basic Statistics > 1 Proportion dialog box in Minitab to see the reliability levels for different sample sizes.  

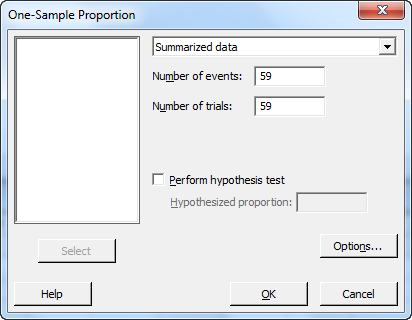
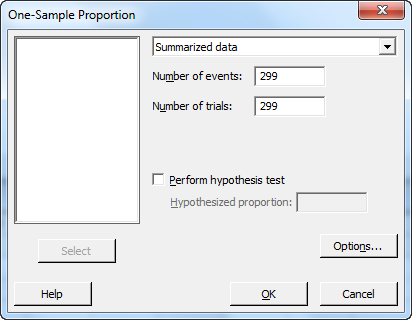
These two sampling plans are really just C=0 Acceptance Sampling plans with an infinite lot size. The same sample sizes can be generated using Stat > Quality Tools > Acceptance Sampling by Attributes by:

1. Setting RQL at 5% for 95% reliability or 1% for 99% reliability.
2. Setting the Consumer’s Risk (β) at 0.05, which results in a 95% confidence level.
3. Setting AQL at an arbitrary value lower than the RQL, such as 0.1%.
4. Setting Producer’s Risk (α) at an arbitrary high value, such as 0.5 (note, α must be less than 1-β to run).

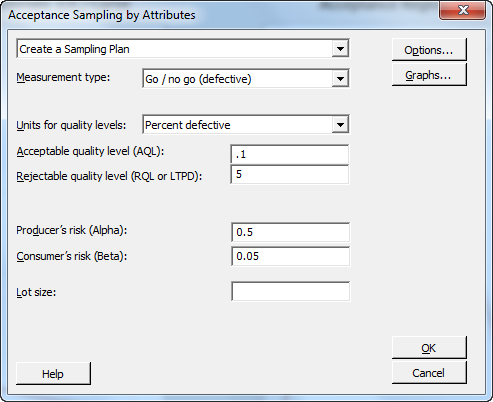
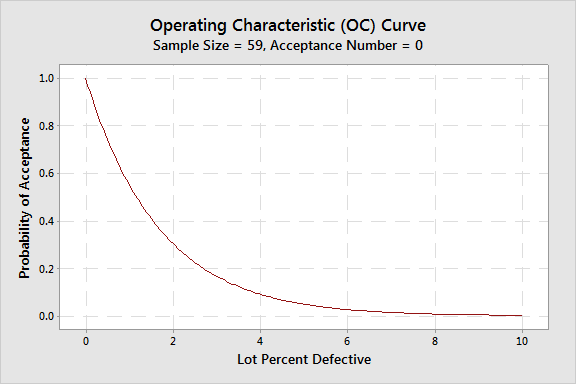
By changing RQL to 1%, the following C=0 plan can be obtained:

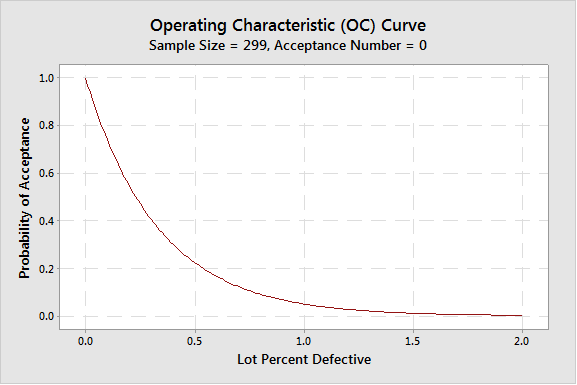
If you want to make the same confidence statements while allowing 1 or more defects in your sample, the sample size required will be larger. For example, allowing 1 defect in the sample will require a sample size of 93 for the 95% reliability statement. This is a C=1 sampling plan. It can be generated, in this case, by lowering the Producer’s risk to 0.05.

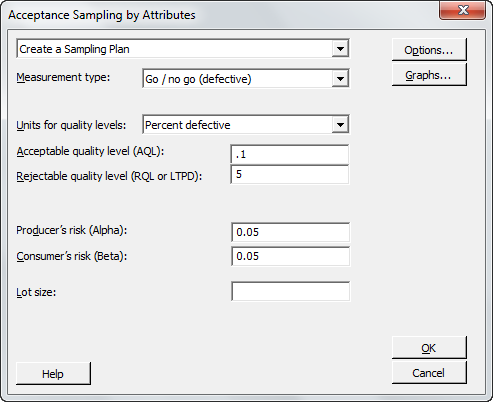
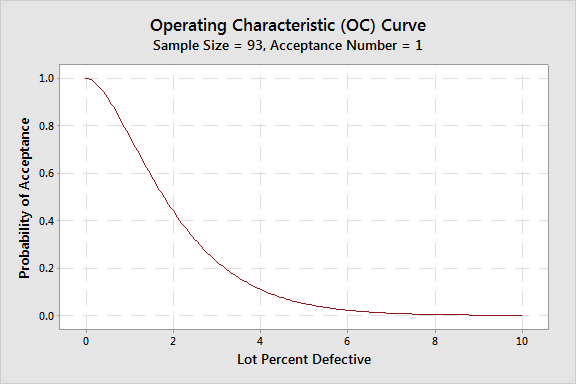
As you can see, the sample size for an acceptance number of 0 is much smaller—in this case, raising the acceptance number from 0 to 1 has raised the sample size from 59 to 93.

Check out this post for more information about acceptance sampling.