By looking at the data we have about 500 cardiac patients, we've learned that easy access to the hospital and good transportation are key factors influencing participation in a rehabilitation program.
Past data shows that each month, about 15 of the patients discharged after cardiac surgery do not have a car. Providing transportation to the hospital might make these patients more likely to join the rehabilitation program, but the costs of such a service can't exceed the potential revenue from participation.We can use the binary logistic regression model developed in part 3 to predict probabilities of participation, to identify where transportation assistance might make the biggest impact, and to develop an estimate of how much we could invest in such assistance.
Download the data set to follow along and try these analyses yourself. If you don't already have Minitab, you can download and use our statistical software free for 30 days.
Using the Regression Model to Predict Patient Participation
We want to develop some estimates of the probability of participation based on whether or not a patient has access to transportation. The first step is make some mesh data representing our population. In Minitab, go to Calc > Create Mesh Data..., and complete the dialog box as shown below. (The maximum and minimum ranges for Age and Distance are drawn directly from the descriptive statistics for the sample data we used to create our regression model.)
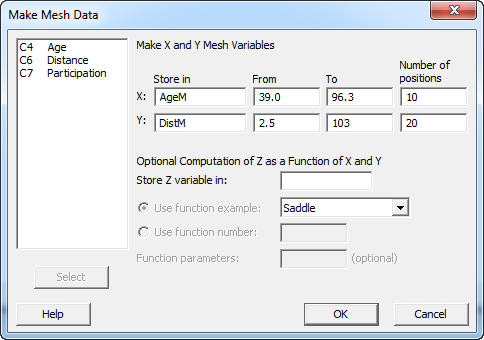
When you press OK, Minitab adds 2 new columns to the worksheet that contain the 200 different combinations of the levels of these factors. Now we'll add two additional columns, one representing patients who have access to a car, and one representing those who don't. Now our worksheet should include four columns of data as shown:
Now we'll go to Stat > Regression > Binary Logistic Regression > Predict... Minitab remembers the last regression model that was run; to make sure it's the right one, click the "View Model..." button...
and confirm that the model displayed is the correct one.
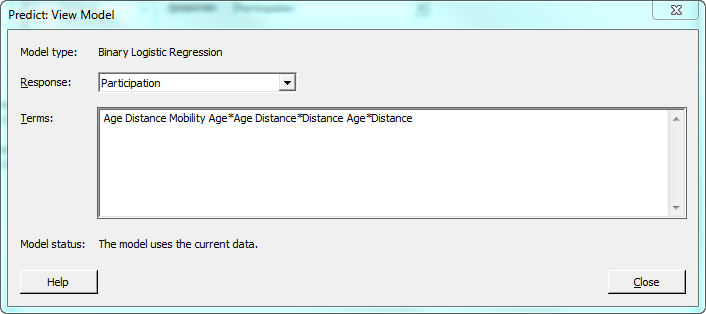
Next, press the "Predict" button and complete the dialog box using the mesh variables we created, as shown. We can also press the "Storage" button to tell Minitab to store the Fits (the predicted probabilities) for each data point in the worksheet. Note that the column selected for the Mobility term is "Car," so all of these predictions will be based on the equation for patients who have access to a vehicle.
When you click OK through all dialogs, Minitab will add a column of data that shows the predicted probability of participation for patients, assuming they have a vehicle.
Now we'll create the predictions for individuals who don't have cars. Press CTRL-E to edit the previous dialog box. This time, for the Mobility column, select "NoCar."
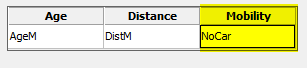
When you press OK, Minitab recalculates the probabilities for the patients, this time using the equation that assumes they do not have a vehicle. The probabilities of participation for each data point are stored in two columns in the worksheet, which I've renamed PFITS-Car and PFITS-No car.
Where Can Providing Transportation Make an Impact?
Now we have estimated probabilities of participation for patients with the same age and distance characteristics, both with and without access to a vehicle. It would be helpful to visualize the differences in these probabilities to see where offering transportation might make the biggest impact in increasing participation rates.
First, we'll use Minitab's calculator to compute the difference in probabilities between having and not having a car. Go to Calc > Calculator... and complete the dialog as shown:
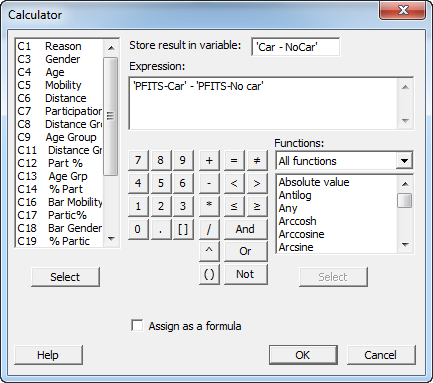
Now we have column of data named "Car - NoCar" that contains the probability difference for patients with the same age and distance characteristics both with and without a vehicle. We can use that column to create a contour plot that offers additional insight into the relationships between the likelihood of participation in the rehabilitation program and a patient's age, distance, and mobility. Select Graph > Contour Plot... and complete the dialog as shown:
Minitab produces this contour plot (we have edited the range of colors from the default):
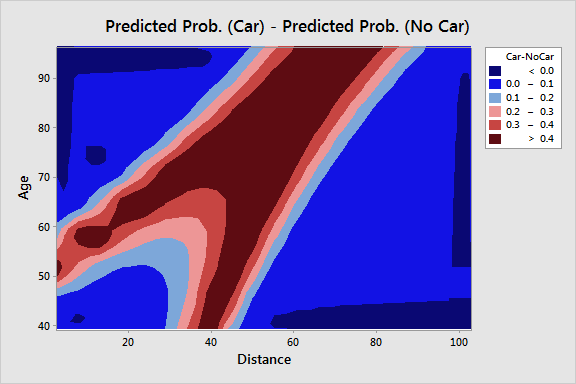
From this plot we can see the patients for whom transportation assistance is likely to make the most impact. These are the patients whose age and distance characteristics fall within the dark-red-colored area, where access to a vehicle raises the probability of participation by more than 40 percent.
The hospital could use this information to carefully target potential recipients of transportation assistance, but doing so would raise many ethical issues. Instead, the hospital will offer transportation assistance to any potential participant who needs it. The project team decides to calculate the average probability of participation for all patients without access to a vehicle.
To obtain that average, select Stat > Basic Statistics > Display Descriptive Statistics... in Minitab, and choose "PFITS-NoCar" as the variable. Click on the "Statistics" button to make sure the Mean is among the descriptive statistics being calculated, and click OK. Minitab will display the descriptive statistics you've selected in the Session Window.
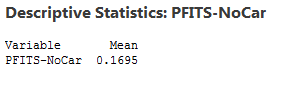
According to our binary logistic regression model, the average probability of participation for all patients without a car equals 0.1695, which we will round up to .17. Now we can easily calculate an estimated break-even point for ensuring transport for patients who need it. We have the following information on hand:
| Patients per month without a car................................................. | 15 |
| Average probability of participation without a car........................... | .30 |
| Average number of sessions per participant.................................. | 29 |
| Revenue per session.................................................................. | $23 |
Based on these figures, a per-patient maximum for transportation can be calculated as:
.17 probability of participation x 29 sessions x $23 per session = $113.39
Since about 15 discharged cardiac patients each month do not have a car, we can invest at most 15 x $113.39 = $1700.85/month in transportation assistance.
Implementing Transportation Assistance for Patient Participation
As described in the article on which inspired this series of posts, the project team evaluated potential improvement options against this this economic calculation and developed a process that brought together patients with cars and those without to carpool to sessions. A pilot-test of the process proved successful, and most of the car-less patients noted that they would not have participated in the rehabilitation program without the service.
After implementing the new carpool process, the project team revisited the key factors they had considered at the start of the initiative, the number of patients enrolling in the program each month, and the average number of sessions participants attended.
After implementing the carpool process, the average number of sessions attended remained constant at 29. But patient participation rose from 33 to 45 per month, which exceeded the project goal of increasing participation to 36 patients per month. Additional revenues turned out to be circa $96,000 annually.
Take-Away Lessons from This Project Study
If you've read all four parts of this series, you may recall that at the start of the Six Sigma project, several stakeholders believed that the problem of low participation could be addressed by creating a nicer brochure for the program, and by encouraging surgeons to tell their patients about it at an earlier point in their treatment.
None of those initial ideas wound up being implemented, but the project team succeeded in meeting the project goals by enacting improvements that were supported by their data analysis. For me, this is a core takeaway from this article.
As the authors note, "Often people’s ideas on processes are incorrect, but improvement actions based on these are still being implemented. These actions cause frustrated employees, may not be cost effective, and in the end do not solve the problem."
Thus, the article makes a compelling case for the value of applying data analysis to improve processes in healthcare. "Even when a somewhat more advanced technique like logistic regression modeling is required," the authors write, "exploratory graphics such as boxplots and bar charts point the direction toward a valuable solution."



