---
title: "Normal: The Kevin Bacon of Distributions"
description: "Normal: The Kevin Bacon of Distributions"
image: https://blog.minitab.com/hubfs/B2BML%20-%20NEW%20FILE%20MANAGER%20STRUCTURE/Blog%20Images/Imported_Blog_Media/eq_1-3.gif
---
English
- [English](https://blog.minitab.com/en/?hsLang=en)
- [Français](https://blog.minitab.com/fr/?hsLang=en)
- [Deutsch](https://blog.minitab.com/de/?hsLang=en)
- [Português](https://blog.minitab.com/pt/?hsLang=en)
- [Español](https://blog.minitab.com/es/?hsLang=en)
- [日本語](https://blog.minitab.com/ja/?hsLang=en)
- [한국어](https://blog.minitab.com/ko/?hsLang=en)
- [中文（简体）](https://blog.minitab.com/zh/?hsLang=en)
- [ Partners](https://www.minitab.com/en-us/company/partners/)
- [ Contact](https://www.minitab.com/en-us/company/contact-us/)
- [ Talk to Minitab](https://www.minitab.com/en-us/talk-to-minitab/)
- [ My Account](https://licensing.minitab.com/account/manage)
[](https://www.minitab.com/en-us/)
- Products
Back
[Products](https://www.minitab.com/en-us/products/)
[All Products](https://www.minitab.com/en-us/products/)
- [Minitab Solution Center](https://www.minitab.com/en-us/products/minitab-solution-center/)
- [Minitab Statistical Software](https://www.minitab.com/en-us/products/minitab/)
- [Minitab Connect](https://www.minitab.com/en-us/products/connect/)
- [Minitab Model Ops](https://www.minitab.com/en-us/products/model-ops/)
- [Minitab Education Hub](https://www.minitab.com/en-us/products/education-hub/)
- [Minitab Engage](https://www.minitab.com/en-us/products/engage/)
- [Minitab Workspace](https://www.minitab.com/en-us/products/workspace/)
- [Real-Time SPC](https://www.minitab.com/en-us/products/real-time-spc/)
- [Prolink Data Collection & SPC](https://www.minitab.com/en-us/products/prolink)
- [Simul8 Discrete Event Simulation](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [SPM](https://www.minitab.com/en-us/products/spm/)
- Solutions
Back
[Solutions](https://www.minitab.com/en-us/solutions/)
[All Solutions](https://www.minitab.com/en-us/solutions/)
- [Analytics](https://www.minitab.com/en-us/solutions/analytics/)
- [Statistics & Predictive Analytics](https://www.minitab.com/en-us/solutions/analytics/statistical-analysis-predictive-analytics/)
- [Data Science & Machine Learning](https://www.minitab.com/en-us/solutions/analytics/data-science-machine-learning/)
- [Business Analytics & Intelligence](https://www.minitab.com/en-us/solutions/analytics/business-analytics-intelligence/)
- [Statistical Process Control](https://www.minitab.com/en-us/solutions/analytics/statistical-process-control/)
- [Quality Analytics](https://www.minitab.com/en-us/solutions/analytics/quality-analytics/)
- [Live Analytics](https://www.minitab.com/en-us/solutions/analytics/live-analytics/)
- [Reliability & Life Data Analysis](https://www.minitab.com/en-us/solutions/analytics/reliability/)
- [Discrete Event Simulation](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [Process Mining](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [Key Capabilities](https://www.minitab.com/en-us/solutions/key-capabilities/)
- [Continuous Improvement](https://www.minitab.com/en-us/solutions/key-capabilities/continuous-improvement/)
- [Data Integration & Data Prep](https://www.minitab.com/en-us/solutions/key-capabilities/data-integration-data-prep/)
- [Diagramming & Mind Mapping](https://www.minitab.com/en-us/solutions/key-capabilities/diagramming-mind-mapping/)
- [Digital Twins](https://info.minitab.com/en/new-to-simul8?hsLang=en)
- [Model Deployment & ML Ops](https://www.minitab.com/en-us/solutions/key-capabilities/model-deployment-ml-ops/)
- [Innovation & Project Management](https://www.minitab.com/en-us/solutions/key-capabilities/innovation-project-management/)
- [Process Excellence: Detect, Correct & Prevent](https://www.minitab.com/en-us/solutions/key-capabilities/process-excellence/)
- [Featured Industries](https://www.minitab.com/en-us/solutions/industry/)
- [Academic](https://www.minitab.com/en-us/solutions/industry/academic/)
- [Energy & Natural Resources](https://www.minitab.com/en-us/solutions/industry/energy-resources/)
- [Government & Public Sector](https://www.minitab.com/en-us/solutions/industry/government/)
- [Healthcare](https://www.minitab.com/en-us/solutions/industry/healthcare/)
- [Insurance](https://www.minitab.com/en-us/solutions/industry/insurance/)
- [Manufacturing & Industrial](https://www.minitab.com/en-us/solutions/industry/manufacturing-industrial/)
- [Services](https://www.minitab.com/en-us/solutions/industry/service-industries/)
- [Software & Technology](https://www.minitab.com/en-us/solutions/industry/software-technology/)
- [Construction](https://www.minitab.com/en-us/solutions/industry/construction/)
- [Featured Roles](https://www.minitab.com/en-us/solutions/role/)
- [Engineering](https://www.minitab.com/en-us/solutions/role/engineering/)
- [Business Analysis](https://www.minitab.com/en-us/solutions/role/business-analysts/)
- [Information Technology](https://www.minitab.com/en-us/solutions/role/information-technology/)
- [Supply Chain](https://www.minitab.com/en-us/solutions/role/supply-chain/)
- [Customer Service & Contact Center](https://www.minitab.com/en-us/solutions/role/customer-service-contact-center/)
- [Human Resources](https://www.minitab.com/en-us/solutions/role/human-resources/)
- [Marketing](https://www.minitab.com/en-us/solutions/role/marketing/)
- [Research and Development](https://www.minitab.com/en-us/solutions/role/research-and-development/)
- Resources & Services
Back
[Resources & Services](https://www.minitab.com/en-us/resources-services/)
[All Resources & Services](https://www.minitab.com/en-us/resources-services/)
- [Resources](https://www.minitab.com/en-us/resources-services/resources/)
- [Case Studies](https://www.minitab.com/en-us/resources-services/resources/case-studies/)
- [eBooks & White Papers](https://www.minitab.com/en-us/resources-services/resources/ebooks-and-white-papers/)
- [Blog](https://blog.minitab.com/blog/?hsLang=en)
- [Data Sets](https://www.minitab.com/en-us/resources-services/resources/data-set/)
- [Webinars & Events](https://www.minitab.com/en-us/resources-services/resources/events/)
- [Education Hub](https://www.minitab.com/en-us/resources-services/resources/education-hub/)
- [Services](https://www.minitab.com/en-us/resources-services/services/)
- [Training](https://www.minitab.com/en-us/resources-services/services/training/)
- [Deployment](https://www.minitab.com/en-us/resources-services/services/deployment/)
- [Consulting](https://www.minitab.com/en-us/resources-services/services/statistical-consulting/)
- [Self-Paced Learning](https://www.minitab.com/en-us/resources-services/services/self-paced-learning/)
- [Continuing Education](https://www.minitab.com/en-us/resources-services/services/continuing-education/)
- Support
Back
[Support](https://www.minitab.com/en-us/support/)
[Technical Support](https://www.minitab.com/en-us/support/)
- [Subscriptions & Activation](https://www.minitab.com/en-us/support/subscriptions-and-activation/)
- [Minitab Quick Start](https://www.minitab.com/en-us/support/quick-start/)
- [Training](https://www.minitab.com/en-us/resources-services/services/training/)
- [Installation Support](https://www.minitab.com/en-us/support/installation/)
- [Support Videos](https://www.minitab.com/en-us/support/videos/)
- [Support Documentation](https://www.minitab.com/en-us/support/documents/)
- [Software Updates](https://www.minitab.com/en-us/support/software-updates/)
- [Product Downloads](https://www.minitab.com/en-us/support/downloads/)
- [Support Policy](https://www.minitab.com/en-us/support/policy/)
- Company
Back
[Company](https://www.minitab.com/en-us/company/)
[Company](https://www.minitab.com/en-us/company/)
- [About Us](https://www.minitab.com/en-us/company/our-company/)
- [Leadership Team](https://www.minitab.com/en-us/company/leadership-team/)
- [Partners](https://www.minitab.com/en-us/company/partners/)
- [Careers](https://www.minitab.com/en-us/company/careers/)
- [Contact](https://www.minitab.com/en-us/company/contact-us/)
- [News](https://www.minitab.com/en-us/company/press-releases/)
[Try/Buy](https://www.minitab.com/en-us/try-buy/)
- [Statistics](https://blog.minitab.com/en/blog/tag/statistics)
- [Data Analysis](https://blog.minitab.com/en/blog/tag/data-analysis)
-
- [Quality Improvement](https://blog.minitab.com/en/blog/tag/quality-improvement)
- [Subscribe](https://info.minitab.com/blog/subscribe?hsLang=en)
## Notice
You are now leaving minitab.com.
Click Continue to proceed to:
Continue
Go Back
# Normal: The Kevin Bacon of Distributions
Minitab Blog Editor | 6/3/2013
Topics: [Statistics](https://blog.minitab.com/en/blog/tag/statistics)
- [Share](https://www.linkedin.com/shareArticle?mini=true&url=https://blog.minitab.com/en/blog/fun-with-statistics/normal-the-kevin-bacon-of-distributions)
- [Share](https://www.facebook.com/sharer.php?u=https://blog.minitab.com/en/blog/fun-with-statistics/normal-the-kevin-bacon-of-distributions)
When you learned statistics, most of what you learned was centered around the Normal distribution. Maybe you became close friends and you later found out his birth name was Gaussian, but either way you probably just call him Normal.
You might know Normal’s a pretty popular guy with plenty of relationships with other distributions. There are some obvious connections, like how eNormal is Lognormal, but I thought I’d share some less obvious ones.
You probably already know that by subtracting his mean and dividing by his standard deviation you get Standard Normal.
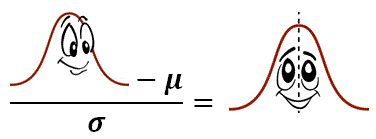
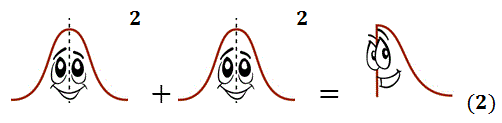
What if you squared Standard Normal? In that case he’d turn right into Chi-Square(1)! And if you have 2 Standard Normal’s? Square them all and add them up and you get Chi-Square(2). In fact you can do this with any number of Standard Normal’s!
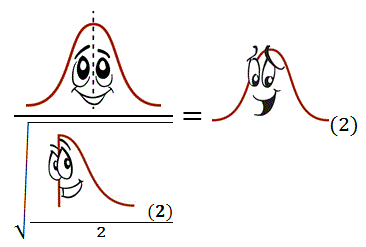
From there it gets a little more complicated. Suppose you divide that Chi-Square(2) by 2 and take the square root. Then you take Standard Normal and divide it by that, and you’re left with T(2) - yep, the same T you use to do t-tests!
Of course we could square that T(2) and suddenly we find ourselves with F(1,2) -- the same F you see at all of those ANOVA parties! But if you’re not a big fan of T and wanted to skip those last few steps, you could have just divided Chi-Square(1) by one and divided that by Chi-Square(2) divided by 2 and you still get F(1,2). So it doesn’t really matter if you were introduced by the Chi-Squares or by the T.
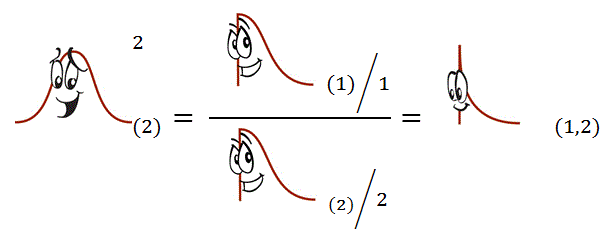
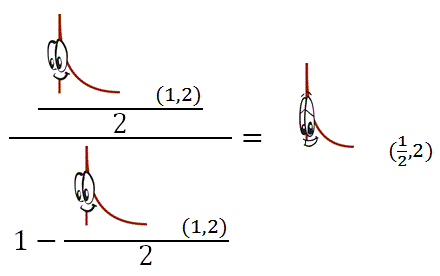
Normal, Standard Normal, Chi-Square, T, and F…these guys are the life of the party and it seems like just about everyone knows them. But F(1,2) has some relatives you probably don’t know. Divide him by 2, and divide that by 1 minus him divided by 2, and you’ll find yourself standing face-to-face with none other than Beta(1/2, 2)!
Beta’s a strange guy. He is so important to so many unique and exciting distributions but usually just stands off by himself trying not to get noticed. Despite all those fun friends he has, his closest relationship might be with boring old Uniform, because Beta(1/2,2) is just a square root away.
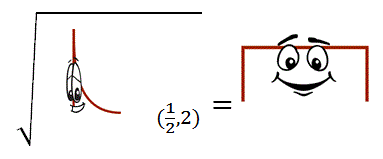
Maybe it’s not fair to call Uniform boring just because of his flat shape and simple distribution function. After all, if you really want to get Uniform excited just take the negative natural log of 1 minus Uniform, raise it to a power, and multiply everything by another number. Maybe you didn’t know he was capable of such complicated things, but if you’ll humor him you’ll suddenly find yourself face-to-face with none other than [Weibull](https://blog.minitab.com/blog/understanding-statistics/chi-square-analysis-of-halloween-and-friday-the-13th-is-there-a-slasher-movie-gender-gap?hsLang=en)!
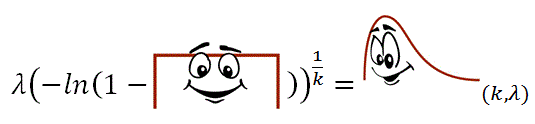
Now Weibull is a really exciting distribution who can take on so many forms and accommodate such a wide variety of processes that you may find him overwhelming. I highly recommend using 1 for that power when changing from Uniform, or if you can’t do that, then raise Weibull to 1 divided by the power you used. Either way you simplify him down to old-fashioned Exponential!
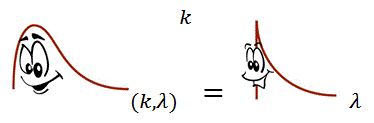
(Quick aside: I never see them together, but you can easily meet Logistic if you know just the right way to work with Exponential or Uniform, and Loglogistic is of course just eLogistic.)
So anyway, Exponential isn’t just a special case of Weibull – he’s a special case of Gamma as well since Exponential(λ) is just Gamma(1,1/λ). Gamma is just like Beta – I bet they’re even related somehow – as he is really important to other distributions but never likes to get up in front of people. If you can get him to talk though, he’ll probably tell you that Gamma(1,1/λ) is just Chi-Square(2) divided by 2λ. Let’s just multiply that by 2λ so we’re left with Chi-Square(2) only.
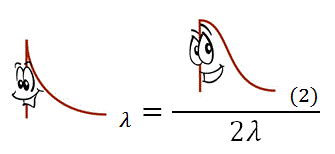
Wait a minute – didn’t we meet Chi-Square(2) earlier? Oh yeah, that’s right…we were introduced right after we squared two Standard Normal’s and added them together! Well either Standard Normal can be turned right back into Normal if we just multiply by a standard deviation and add a mean, but if we did that we’d just be left with…
…the Normal distribution.
So did we just meet 13 different distributions, or 13 variations on Normal?
*Author's note: A huge thanks to our graphics guru Trevor Calabro, who turned a ridiculous blog post into a ridiculous blog post with awesome graphics!*
## You Might Also Like
[IT vs. OT: Unlocking the Power of Convergence](https://blog.minitab.com/en/blog/it-vs.-ot-unlocking-the-power-of-convergence?hsLang=en)
[Operations](https://blog.minitab.com/en/blog/tag/operations) | 6 Minute Read
[Updating Graphs, Making Patterned Data and More Tips & Tricks to Help You Master Minitab](https://blog.minitab.com/en/blog/updating-graphs-patterned-data-tips-tricks-master-minitab?hsLang=en)
[Statistics](https://blog.minitab.com/en/blog/tag/statistics) | 6 Minute Read
[Against the Odds: Honoring Women in Math and Statistics](https://blog.minitab.com/en/blog/honoring-women-in-math-and-statistics?hsLang=en)
[Statistics](https://blog.minitab.com/en/blog/tag/statistics) | 5 Minute Read
---
- [Careers](https://www.minitab.com/en-us/company/careers/)
- [Trust Center](https://www.minitab.com/en-us/trust-center/)
- [Suppliers](https://www.minitab.com/en-us/suppliers/)
- [Site Map](https://www.minitab.com/en-us/site-map/)
- [](https://www.linkedin.com/company/minitab/)
- [](https://www.facebook.com/Minitab/)
- [](https://www.youtube.com/user/MinitabInc)
- [](https://www.instagram.com/minitab/)
---
© 2025 Minitab, LLC. All Rights Reserved.
- [Terms of Use](https://www.minitab.com/en-us/legal/terms-of-use/)
- [Privacy Policy](https://www.minitab.com/en-us/legal/privacy-policy/)
- [Legal](https://www.minitab.com/en-us/legal/)
- Cookies Settings