Every now and then I’ll test my Internet speed at home using such sites as http://speedtest.comcast.net. My need to perform these tests could stem from the cool-looking interfaces they employ on their site, as they display the results using analog speedometers and RPM meters. They could also stem from the validation that I need in "getting what I am paying for," although I realize that there are other factors that determine what Internet speed you ultimately end up with when you browse the Web.
Recently I started thinking about the distribution of these speeds. If I were to run enough tests, would these speeds be normally distributed?
When performing an Internet speed test, you are given an estimated download and upload speed. The download speed is the rate at which data travels from the Internet to your device, and the upload speed is the rate at which data travels from your device to the Internet. I was also curious as to whether the population means of these speeds were statistically different.
Is the Data Normally Distributed?
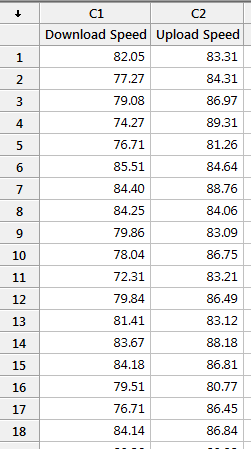
I ran 30 speed tests from my office at Minitab and recorded the download and upload data into a Minitab Statistical Software worksheet: Here is a sample of the data:
I went to Stat > Basic Statistics > Normality Test. Here are the probability plots for download and upload speed.
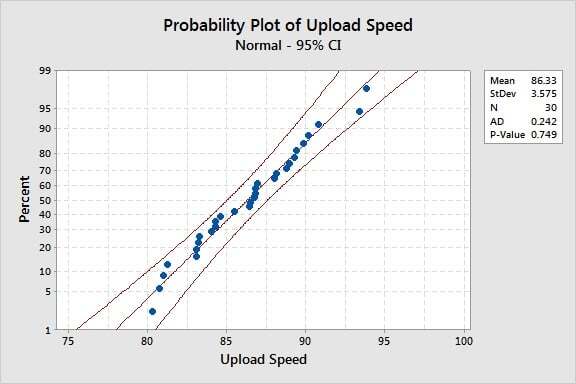
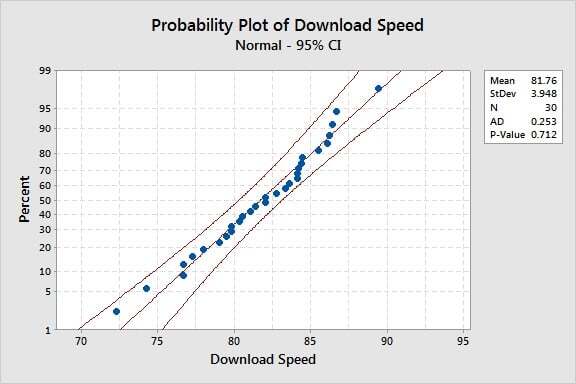
I’ll be using an alpha level of 0.05 to compare the p-value to. Both probability plots show p-values greater than alpha, and therefore we do not have enough evidence to reject the null hypothesis. As a quick reminder, the null hypothesis is that our data follows a normal distribution. We can assume normality.
Is There a Difference Between Upload and Download Speed?
Let’s find out if there was a statistical difference between the download speed and the upload speed.
Go to Stat > Basic Statistics > 2-Sample t:
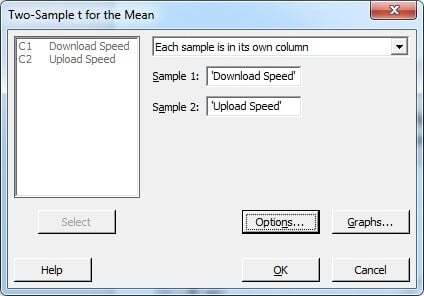
I chose “Each Sample is in its own column” under the dropdown, and entered in the column for download speed for Sample 1 and upload speed for Sample 2.
If you click on Options you’ll see a checkbox for "Assume Equal Variances." Checking this box will result in a slightly more powerful 2-Sample-t test. But how do I know if the variances are equal or not? By using quick test in Minitab!
I cancelled out of the 2-Sample t dialog window and quickly ran an Equal Variances test (Stat > Basic Statistics > 2 Variances) and received these results:

Given that our p-value is greater than an alpha of 0.05, we don’t have enough evidence to say that the two variances are statistically different. Therefore, we are able to go back to the 2-Sample t test and check the box for "Assume equal Variances."
Here's the output from my 2-Sample t-test:
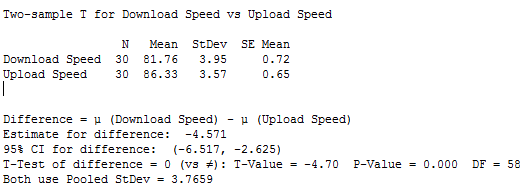
Since our p-value is less than 0.05, we can reject the null hypothesis (that both means are the same) and say that the population means for download and upload speed are statistically different.
Vrrrrooooooooom!
I was curious as to why the upload speeds were higher than the download speeds during my testing. Whenever I’ve tested speeds at my house, I’ve always seen the reverse.
I asked someone here at Minitab who is well versed in network setup, and he said that there could have been more bandwidth consumption from my coworkers than normal at the time of data collection. This extra consumption can push the download speeds below the upload speeds. He also said that the nature of how the Internet is configured at a company can be a contributing factor as well.
If you were given an expected download rate by your cable company, you could add to this experiment by performing a 1-Sample t-test. The expected download rate would serve as your hypothesized mean. You would then be able to perform a hypothesis test to see if your mean is statistically different from your hypothesized mean.
If you find that you're not getting the speeds you wanted, I wouldn't start running around with pitchforks just yet. According to http://www.cnet.com/how-to/how-to-find-a-reliable-network-speed-test/ , accuracy and consistency in speeds may depend on what online speed test you are using. But comparing the different speed testing tools is an analysis for another day!



