If you’re a quality improvement expert, you already know that statistics can be a powerful tool in your quest to reduce the cost of poor quality and save money. But statistics might be even more powerful than you think—it may actually have helped someone win a lottery jackpot.
According to Business Insider, a former mathematics professor with a Ph.D. in statistics has won the Texas lottery four times, with multi-million dollar payouts each time. The article speculates whether she’s super lucky, or whether she’s used public information and her knowledge of statistics to identify patterns that allow her to beat the odds.
Regardless of how she won, it’s certainly true that looking for patterns is an important strategy in statistics. And graphs are a great way to see patterns in your data quickly and easily.
Here are five patterns that Minitab graphs can help you detect--and what each pattern means.
PATTERN 1: Points that fall within a “fat pencil” on a normal probability plot
You’ll often see the normality plot in Minitab output for analyses that are theoretically based on the normal distribution, such as normal capability analysis.
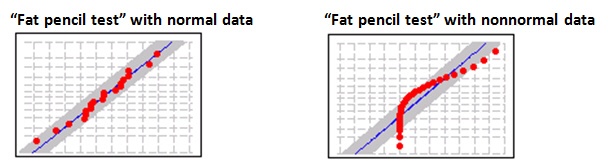
Imagine a fat pencil lying on top of the fitted line: if it covers all the data points on the plot, the data is probably normal; if points are far enough from the fitted line that they are visible beyond the edges of the fat pencil, the data is probably nonnormal.
PATTERN 2: Points that don't vary randomly on a control chart
A control chart monitors the stability of your process. If the points fall randomly within the control limits, without any discernible pattern, your process is in control.

But if you notice a nonrandom pattern in the chart, such as a pattern that “repeats” itself, or variation that gets increasingly large:

or a “shift” or “drift” in the process:

....then your process may be out-of-kilter. Minitab also tests for special causes that identify specific nonrandom patterns.
PATTERN 3: Points that follow straight or curved lines on a scatterplot
Different types of models reflect specific trends in your data. The type of model you use affects how accurately it describes your data and how well it predicts how an input variable will affect the output variable.

Selecting the right type of model is important when you perform regression, trend analysis, response surface analysis, and general linear models.
PATTERN 4: Points that form parallel lines on an interaction plot
You can use interaction plots to see potential interactions between factors. For example, an engineer might want to know if temperature and pressure interact together to affect the strength of a product material. Parallel lines indicate the factors do not interact to affect the response.

The greater the difference in slope between the lines, the greater the possible interaction between the factors.

In Minitab, you can display interaction plots when you use analyses that compare the response among different levels of two or more factors, such as ANOVA (Analysis of Variance) or DOE (Design of Experiments).
PATTERN 5: Points that form a cowboy hat on a 3D plot

This pattern means you may need to round up some stray cattle in your process, pilgrim.
Just kidding, of course. But Minitab does have some great 3D graphing features to visualize relationships among 3 variables. Try experimenting with them to learn more about their capability.
For example, it’s really easy to make a cowboy hat and spin it around. In fact, it’s almost as much fun as winning the Texas lottery.
(To create the 3D data, choose Calc > Make Mesh Data, use the “Cowboy Hat” function example, and store x, y, and z in worksheet columns c1, c2, and c3, respectively. After the mesh data is in your worksheet, choose Graph > 3D Surface Plot and enter the columns for x, y, z. Use the 3D tools (arrows) to rotate the plot.)



