Overfitting a model is a real problem you need to beware of when performing regression analysis. An overfit model result in misleading regression coefficients, p-values, and R-squared statistics. Nobody wants that, so let's examine what overfit models are, and how to avoid falling into the overfitting trap.
Put simply, an overfit model is too complex for the data you're analyzing. Rather than reflecting the entire population, an overfit regression model is perfectly suited to the noise, anomalies, and random features of the specific sample you've collected. When that happens, the overfit model is unlikely to fit another random sample drawn from the same population, which would have its own quirks.
A good model should fit not just the sample you have, but any new samples you collect from the same population.
For an example of the dangers of overfitting regression models, take a look at this fitted line plot:
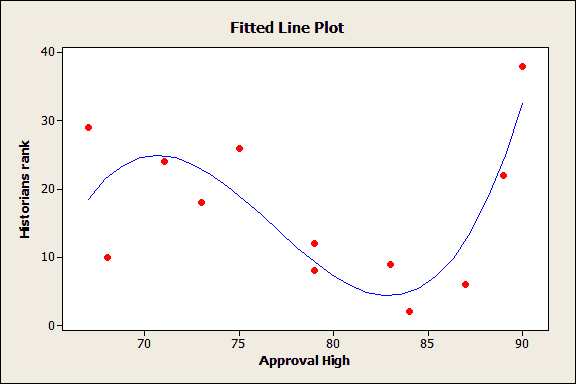
Even though this model looks like it explains a lot of variation in the response, it's too complicated for this sample data. In the population, there is no true relationship between the predictor and this response, as is explained in detail here.
Basics of Inferential Statistics
For more insight into the problems with overfitting, let's review a basic concept of inferential statistics, in which we try to draw conclusions about a population from a random sample. The sample data is used to provide unbiased estimates of population parameters and relationships, and also in testing hypotheses about the population.
In inferential statistics, the size of your sample affects the amount of information you can glean about the population. If you want to learn more, you need larger sample sizes. Trying to wrest too much information from a small sample isn't going to work very well.
For example, with a sample size of 20, you could probably get a good estimate of a single population mean. But estimating two population means with a total sample size of 20 is a riskier proposition. If you want to estimate three or more population means with that same sample, any conclusions you draw are going to be pretty sketchy.
In other words, trying to learn too much from a sample leads to results that aren't as reliable as we'd like. In this example, as the observations per parameter decreases from 20 to 10 to 6.7 and beyond, the parameter estimates will become more unreliable. A new sample would likely yield different parameter estimates.
How Sample Size Relates to an Overfit Model
Similarly, overfitting a regression model results from trying to estimate too many parameters from too small a sample. In regression, a single sample is used to estimate the coefficients for all of the terms in the model. That includes every predictor, interaction, and polynomial term. As a result, the number of terms your can safely accommodate depends on the size of your sample.
Larger samples permit more complex models, so if the question or process you're investigating is very complicated, you'll need a sample size large enough to support that complexity. With an inadequate sample size, your model won't be trustworthy.
So your sample needs enough observations for each term. In multiple linear regression, 10-15 observations per term is a good rule of thumb. A model with two predictors and an interaction, therefore, would require 30 to 45 observations—perhaps more if you have high multicollinearity or a small effect size.
Avoiding Overfit Models
You can detect overfit through cross-validation—determining how well your model fits new observations. Partitioning your data is one way to assess how the model fits observations that weren't used to estimate the model.
For linear models, Minitab calculates predicted R-squared, a cross-validation method that doesn't require a separate sample. To calculate predicted R-squared, Minitab systematically removes each observation from the data set, estimates the regression equation, and determines how well the model predicts the removed observation.
A model that performs poorly at predicting the removed observations probably conforms to the specific data points in the sample, and can't be generalized to the full population.
The best solution to an overfitting problem is avoidance. Identify the important variables and think about the model that you are likely to specify, then plan ahead to collect a sample large enough handle all predictors, interactions, and polynomial terms your response variable might require.
Jim Frost discusses offers some good advice about selecting a model in How to Choose the Best Regression Model. Also, check out his post about how too many phantom degrees of freedom can lead to overfitting, too.



