Every day brings news about this poll or that survey and what it means. News reports about public opinion are particularly thick during election years, when it seems like barely an hour goes by without new poll results claiming to reveal the current state of the electorate.
But a great deal of the insight that can be derived from political polling data—or any public opinion research, for that matter—rarely makes it into the press. One source of insight is the use of cross tabulation and Chi-Square analysis, which we can use to summarize observations by categories. For example, the news may report that a larger percentage of those surveyed prefer this or that candidate, but they less frequently drill down to report whether, for instance, there's an association between a certain characteristic and candidate preference.
But that's the kind of actionable insight that campaign consultants, advertisers, and almost anyone else who does a survey really wants to know. It also has applications in the quality improvement and customer service arenas, where this type of data analysis can reveal whether there's an association between, for example, customers' gender and the type of services they use.
Statistical Association between Categorical Variables Like Gender and Political Affiliation
To do a cross tabulation and Chi Square analysis, you'll need to collect data on some categorical variables.
For instance, political surveys frequently ask respondents to provide gender, educational level, and income bracket. If you're analyzing that data in Minitab Statistical Software, you'd give each categorical variable its own column, with each row representing one respondent in your survey.
Let's say you're working on a campaign for the Bull Moose Party and you want to find out whether there's an association between gender and candidate preference. So you survey 400 randomly selected voters and enter your data so it looks like the columns you see on the right. (Download the simulated data here if you'd like to play along.)
To analyze this data, you choose Stat > Tables > Cross Tabulation and Chi-Square in Minitab. Minitab asks you select the variable that will correspond to the table's rows and the table's columns. We'll choose "Gender" for rows and "Affiliation" for columns.
If we click "OK" now, Minitab provides a table that shows the cross-tabbed counts of each variable:
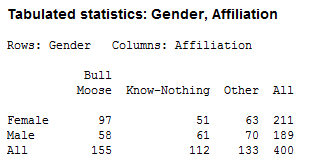
Eyeballing this table, it does look like there might be an association between the Bull Moose Party and the women surveyed. Interesting, but the count data alone can't tell us if there's really a statistical association between gender and party affiliation or not. For that, we need to do the full Chi-Square analysis.
Basic Chi-Square Analysis
The Chi-Square test helps you determine if two discrete variables are associated. If there's an association, the distribution of one variable will differ depending on the value of the second variable. But if the two variables are independent, the distribution of the first variable will be similar for all values of the second variable.
Let's go back into the Stat > Tables > Cross Tabulation and Chi-Square dialog. This time, click on the Chi-Square... button. Check the options for Chi-Square analysis and Expected cell counts, then press OK, and OK again to run the analysis. Minitab gives the following output:
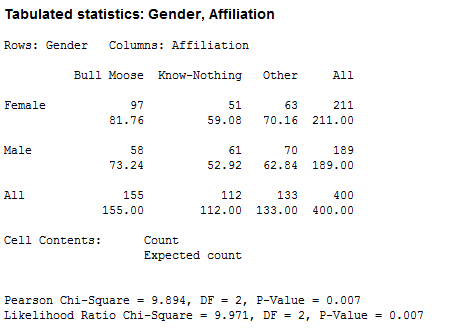
- If the p-value is less than or equal to alpha, the variables are associated.
- If the p-value is greater than alpha, you can conclude that they're independent.
Beyond Chi-Square: Other Measures of Association



