Por Matthew Barsalou, blogger invitado
Enseñar a usar los estudios de rendimiento y capacidad del proceso es más fácil cuando se dispone de datos de procesos reales para que el estudiante o el aprendiz practique. Como he señalado anteriormente en el Blog de Minitab, se puede usar una catapulta para generar datos para un estudio de capacidad. Mi último blog sobre cómo usar una catapulta para este propósito fue hace varios años, así que me gustaría volver al tema haciendo énfasis en cómo interpretar los resultados del estudio de la catapulta en la herramienta Capability SixpackTM de Minitab Statistical Software. La catapulta puede utilizarse con diversas configuraciones, pero aquí la configuración se mantendrá constante para simular un proceso de manufactura. Los planos y las instrucciones de montaje están disponibles aquí.
El estudio de la catapulta
En la catapulta se utilizó una banda elástica súper resistente de 120 mm de diámetro diseñada originalmente para su uso en aeromodelismo. La guía de la banda se fijó en 4 cm y el tope del brazo se fijó en 1 cm. El punto de partida se fijó en 8 cm y estos ajustes se mantuvieron constantes durante todo el estudio. Tres operadores realizaron 2 corridas de 20 disparos cada uno para simular dos días de producción con tres turnos por día. Cada corrida se utilizó para un subgrupo separado en el estudio de capacidad y rendimiento.
Los índices de capacidad Cp y Cpk utilizan datos a corto plazo para indicarnos lo que el proceso es capaz de hacer y los índices de rendimiento Pp y Ppk utilizan datos a largo plazo que nos indican lo que el proceso está haciendo realmente. Los índices de capacidad utilizan la variación “a corto plazo” en la fórmula, mientras que los índices de rendimiento usan la variación “a largo plazo”; la variación a corto plazo se basa en las desviaciones estándar agrupadas de los subgrupos y la variación a largo plazo se basa en la desviación estándar de todo el conjunto de datos.
Hay requisitos que se deben cumplir para realizar un estudio de capacidad o rendimiento. Los datos deben estar distribuidos normalmente y el proceso debe encontrarse en un estado de control estadístico. Además, los datos se deben seleccionar de forma aleatoria y deben representar a la población. El conjunto de datos debe contener por lo menos 100 valores; de lo contrario, el intervalo de confianza para los valores resultantes de capacidad y rendimiento será muy amplio. La persona que planifique el estudio debe asegurarse de que existan suficientes datos y que los datos representen los valores de la población; sin embargo, la herramienta Capability Sixpack de Minitab Statistical Software se puede utilizar para asegurar que se cumplan los demás requisitos.
La siguiente figura muestra un análisis Capability Sixpack para el estudio sobre la catapulta.
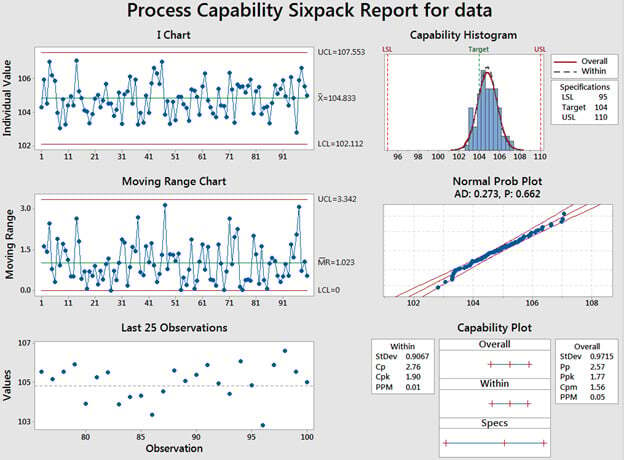
El análisis Capability Sixpack
El análisis Capability Sixpack proporciona una gráfica I cuando los datos son valores individuales; es decir, cuando el tamaño del subgrupo es 1. Cuando los datos se ingresan como subgrupos, se proporciona una gráfica Xbarra. Cualquiera de las dos gráficas de control puede utilizarse para evaluar la estabilidad del proceso. Si se observan valores fuera de control en una gráfica de control, eso significa que habrá que mejorar el proceso para lograr la estabilidad. Se debe buscar y eliminar la fuente de variabilidad en el proceso y luego se debe repetir el estudio.
Cuando el tamaño del subgrupo es 1, se muestra una gráfica de rangos móviles, pero cuando el tamaño del subgrupo es mayor que 1 se incluye una gráfica S. Los valores de la gráfica de rangos móviles se deben comparar con los valores de la gráfica I para comprobar que no existan patrones. Si se utilizan las gráficas Xbarra y S, se debe hacer la comparación entre ellas. Esto permite asegurar que los datos sean realmente aleatorios. Se mostrarán las últimas 25 observaciones o los últimos 5 subgrupos. Las últimas 25 observaciones se muestran si los datos se ingresan como 1 subgrupo, mientras que los últimos 5 subgrupos se muestran si los datos son ingresan como subgrupos. Los valores deben verse como datos aleatorios y sin tendencias o cambios rápidos si el proceso es estable.
Se muestra un histograma de capacidad para comparar el histograma de los datos con los límites de especificación. Los datos deben aproximarse a la distribución normal estándar. La línea de “largo plazo” muestra la forma de un histograma utilizando la desviación estándar a largo plazo. La línea de “corto plazo” muestra la forma del histograma utilizando la desviación estándar agrupada de los subgrupos.
Se proporciona una gráfica de probabilidad normal para evaluar la normalidad de los datos. Un valor p de menos de 0.05 indica que los datos no están distribuidos normalmente. Si los datos no están distribuidos normalmente, no se pueden utilizar en un estudio de capacidad. Los datos no normales se pueden transformar o se puede identificar y eliminar la causa de la falta de normalidad. La mejor opción es mejorar el proceso para que los datos estén distribuidos normalmente. El análisis Capability Sixpack no se puede utilizar si los datos alcanzan un límite como el 0 o un límite superior o inferior; sin embargo, se puede usar la opción de estudio de capacidad regular ya que se coloca una marca de verificación junto al indicador de límite al lado del límite de especificación.
La gráfica de capacidad muestra la capacidad y el rendimiento del proceso. La capacidad de un proceso se mide usando el Cp y el Cpk, y ambos índices nos indican de qué es capaz el proceso. Están diseñados para su uso con datos a corto plazo y utilizan la desviación estándar agrupada de los subgrupos racionales para decirnos de qué es capaz el proceso. Los subgrupos racionales utilizan datos homogéneos para que solo exista variación por causas comunes. Por ejemplo, todas las partes pueden haber sido producidas en la misma máquina, usando el mismo lote de materia prima, por el mismo operador. El Cp compara la dispersión del proceso hacia los límites de especificación; un proceso con un valor de Cp alto puede producir partes fuera de las especificaciones si el proceso no está centrado. El Cpk considera la posición de la media del proceso en relación con límites de especificación y en realidad existen dos valores para el Cpk: el Cpk del límite de especificación superior y el Cpk del límite de especificación inferior. De los dos valores de Cpk, el análisis Capability Sixpack muestra el valor de peor rendimiento.
El rendimiento de un proceso se mide usando el Pp y el Ppk con datos a largo plazo. Por lo general, se deben usar datos de producción de más de 30 días para el Pp y el Ppk. A diferencia de los índices de capacidad Cp y Cpk, los cálculos de Pp y Ppk se realizan utilizando la desviación estándar total, que es igual que la fórmula para una desviación estándar de la muestra. El Pp compara la dispersión del proceso hacia los límites de especificación superior e inferior y solo se proporciona el valor de peor rendimiento. El Ppk considera la posición de la media del proceso en relación con límites de especificación.
El índice de capacidad del proceso de la media es el Cpm, que utiliza un valor objetivo para representar la media del proceso en relación con el objetivo. Sin embargo, esto solo se proporciona si se ingresa un valor objetivo en Minitab.
Conclusión
El análisis Capability Sixpack de Minitab proporciona un estudio de capacidad rápido y fácil; sin embargo, no indica directamente si los datos son inestables para un estudio de capacidad. No obstante, ofrece métodos para evaluar la idoneidad de los datos que deben utilizarse cada vez que se realiza un estudio de capacidad.
Matthew Barsalou se desempeña como master black belt en resolución de problemas estadísticos en BorgWarner Turbo Systems Engineering GmbH. Es master black belt en Six Sigma Esbelto certificado por Smarter Solutions, black belt en Six Sigma, ingeniero de control de calidad y técnico de control calidad certificado por la ASQ y gerente de control de calidad, representante de gestión de calidad y auditor certificado por TÜV. Posee una licenciatura en Ciencias industriales, una maestría en Estudios liberales con énfasis en Negocios internacionales y también cuenta con una maestría en Administración de empresas e ingeniería comercial del Wilhelm Büchner Hochschule de Darmstadt, Alemania. Es autor de los libros Root Cause Analysis: A Step-By-Step Guide to Using the Right Tool at the Right Time, Statistics for Six Sigma Black Belts y The ASQ Pocket Guide to Statistics for Six Sigma Black Belts.



